Advertisements
Advertisements
प्रश्न
Use ruler and compass only for the following question. All construction lines and arcs must be clearly shown.
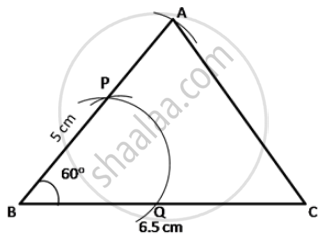
- Construct a ΔABC in which BC = 6.5 cm, ∠ABC = 60°, AB = 5 cm.
- Construct the locus of points at a distance of 3.5 cm from A.
- Construct the locus of points equidistant from AC and BC.
- Mark 2 points X and Y which are at a distance of 3.5 cm from A and also equidistant from AC and BC. Measure XY.
उत्तर
- Steps of construction:
- Draw BC = 6.5 cm using a ruler.
- With B as center and radius equal to approximately half of BC, draw an arc that cuts the segment BC at Q.
- With Q as center and same radius, cut the previous arc at P.
- Join BP and extend it.
- With B as center and radius 5 cm, draw an arc that cuts the arm PB to obtain point A.
- Join AC to obtain ΔABC.
- With A as center and radius 3.5 cm, draw a circle.
The circumference of a circle is the required locus.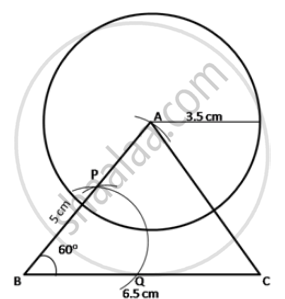
- Draw CH, which is bisector of ΔACB. CH is the required locus.
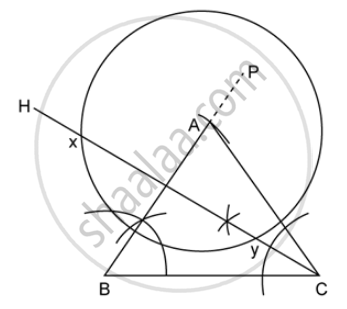
- Circle with center A and line CH meet at points X and Y as shown in the figure. xy = 5 cm (approximately).
APPEARS IN
संबंधित प्रश्न
Construct a triangle ABC, with AB = 5.6 cm, AC = BC = 9.2 cm. Find the points equidistant from AB and AC; and also 2 cm from BC. Measure the distance between the two points obtained.
Construct an isosceles triangle ABC such that AB = 6 cm, BC = AC = 4 cm. Bisect ∠C internally and mark a point P on this bisector such that CP = 5 cm. Find the points Q and R which are 5 cm from P and also 5 cm from the line AB.
Two straight roads AB and CD cross each other at Pat an angle of 75° . X is a stone on the road AB, 800m from P towards B. BY taking an appropriate scale draw a figure to locate the position of a pole, which is equidistant from P and X, and is also equidistant from the roads.
In Δ PQR, s is a point on PR such that ∠ PQS = ∠ RQS . Prove thats is equidistant from PQ and QR.
In Δ PQR, bisectors of ∠ PQR and ∠ PRQ meet at I. Prove that I is equidistant from the three sides of the triangle , and PI bisects ∠ QPR .
Draw and describe the lorus in the following cases:
The locus of points at a distance of 4 cm from a fixed line.
Draw and describe the lorus in the following cases:
The lorus of a point in rhombus ABCD which is equidistant from AB and AD .
Construct a triangle BPC given BC = 5 cm, BP = 4 cm and .
i) complete the rectangle ABCD such that:
a) P is equidistant from AB and BCV
b) P is equidistant from C and D.
ii) Measure and record the length of AB.
Using only a ruler and compass construct ∠ABC = 120°, where AB = BC = 5 cm.
(i) Mark two points D and E which satisfy the condition that they are equidistant from both ABA and BC.
(ii) In the above figure, join AD, DC, AE and EC. Describe the figures:
(a) AECB, (b) ABD, (c) ABE.
Given ∠BAC (Fig), determine the locus of a point which lies in the interior of ∠BAC and equidistant from two lines AB and AC.
