Advertisements
Advertisements
प्रश्न
Construct a rhombus ABCD whose diagonals AC and BD are 8 cm and 6 cm respectively. Find by construction a point P equidistant from AB and AD and also from C and D.
उत्तर

Steps of Construction:
(i) Draw BC = 6 cm.
(ii) Draw AD = 8 on perpendicular to BC.
(iii) With B as centre draw arcs on AD.
(iv) With C as centre draw arcs on AD. ABCD is the required rhombus.
(v) Draw perpendicular bisectors of AB, and CD, which meet at 0.
(vi) Since AD and BC are diagonals of rhombus and meet at 0.
AO = OD
O is the point equidistant from AB, AD and C, D.
APPEARS IN
संबंधित प्रश्न
Describe the locus of vertices of all isosceles triangles having a common base.
Describe the locus of a point P, so that:
AB2 = AP2 + BP2,
where A and B are two fixed points.
Draw two intersecting lines to include an angle of 30°. Use ruler and compasses to locate points which are equidistant from these Iines and also 2 cm away from their point of intersection. How many such points exist?
AB and CD are two intersecting lines. Find a point equidistant from AB and CD, and also at a distance of 1.8 cm from another given line EF.
A and B are fixed points while Pis a moving point, moving in a way that it is always equidistant from A and B. What is the locus of the path traced out by the pcint P?
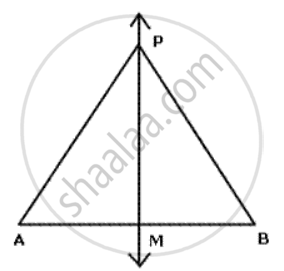
Draw and describe the lorus in the following cases:
The lorus of points inside a circle and equidistant from two fixed points on the circle .
Construct a triangle BPC given BC = 5 cm, BP = 4 cm and .
i) complete the rectangle ABCD such that:
a) P is equidistant from AB and BCV
b) P is equidistant from C and D.
ii) Measure and record the length of AB.
Without using set squares or protractor construct a triangle ABC in which AB = 4 cm, BC = 5 cm and ∠ABC = 120°.
(i) Locate the point P such that ∠BAp = 90° and BP = CP.
(ii) Measure the length of BP.
Using ruler and compasses construct:
(i) a triangle ABC in which AB = 5.5 cm, BC = 3.4 cm and CA = 4.9 cm.
(ii) the locus of point equidistant from A and C.
(iii) a circle touching AB at A and passing through C.
Given ∠BAC (Fig), determine the locus of a point which lies in the interior of ∠BAC and equidistant from two lines AB and AC.
