Advertisements
Advertisements
प्रश्न
State and draw the locus of a swimmer maintaining the same distance from a lighthouse.
उत्तर
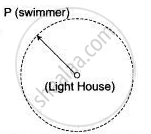
Proof: The locus of the swimmer will be a circle with light house as the centre and the same distance between the light house and the swimmer as radius.
APPEARS IN
संबंधित प्रश्न
Construct a triangle ABC with AB = 5.5 cm, AC = 6 cm and ∠BAC = 105°
Hence:
1) Construct the locus of points equidistant from BA and BC
2) Construct the locus of points equidistant from B and C.
3) Mark the point which satisfies the above two loci as P. Measure and write the length of PC.
On a graph paper, draw the lines x = 3 and y = –5. Now, on the same graph paper, draw the locus of the point which is equidistant from the given lines.
AB and CD are two intersecting lines. Find a point equidistant from AB and CD, and also at a distance of 1.8 cm from another given line EF.
Construct a rhombus ABCD whose diagonals AC and BD are 8 cm and 6 cm respectively. Find by construction a point P equidistant from AB and AD and also from C and D.
In Δ PQR, bisectors of ∠ PQR and ∠ PRQ meet at I. Prove that I is equidistant from the three sides of the triangle , and PI bisects ∠ QPR .
Draw and describe the lorus in the following cases:
The locus of points at a distance of 4 cm from a fixed line.
Describe completely the locus of point in the following cases:
Midpoint of radii of a circle.
Describe completely the locus of points in the following cases:
Centre of a circle of varying radius and touching the two arms of ∠ ABC.
Describe completely the locus of points in the following cases:
Centre of a cirde of radius 2 cm and touching a fixed circle of radius 3 cm with centre O.
Using a ruler and compass only:
(i) Construct a triangle ABC with BC = 6 cm, ∠ABC = 120° and AB = 3.5 cm.
(ii) In the above figure, draw a circle with BC as diameter. Find a point 'P' on the circumference of the circle which is equidistant from Ab and BC.
Measure ∠BCP.
