Advertisements
Advertisements
प्रश्न
Describe the locus of the centres of all circles passing through two fixed points.
उत्तर
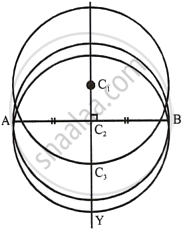
The locus of the centre of all the circles which pass through two fixed points will be the perpendicular bisector of the line segment joining the two fixed points which are given.
APPEARS IN
संबंधित प्रश्न
In the figure given below, find a point P on CD equidistant from points A and B.

Describe the locus of points at a distance 2 cm from a fixed line.
Describe the locus of a stone dropped from the top of a tower.
Describe the locus of points at distances less than 3 cm from a given point.
Describe the locus of points at distances greater than or equal to 35 mm from a given point.
Sketch and describe the locus of the vertices of all triangles with a given base and a given altitude.
By actual drawing obtain the points equidistant from lines m and n; and 6 cm from a point P, where P is 2 cm above m, m is parallel to n and m is 6 cm above n.
Draw a triangle ABC in which AB = 6 cm, BC = 4.5 cm and AC = 5 cm. Draw and label:
- the locus of the centres of all circles which touch AB and AC,
- the locus of the centres of all the circles of radius 2 cm which touch AB.
Hence, construct the circle of radius 2 cm which touches AB and AC .
The bisectors of ∠B and ∠C of a quadrilateral ABCD intersect in P. Show that P is equidistant from the opposite sides AB and CD.
Use ruler and compasses for the following question taking a scale of 10 m = 1 cm. A park in a city is bounded by straight fences AB, BC, CD and DA. Given that AB = 50 m, BC = 63 m, ∠ABC = 75°. D is a point equidistant from the fences AB and BC. If ∠BAD = 90°, construct the outline of the park ABCD. Also locate a point P on the line BD for the flag post which is equidistant from the corners of the park A and B.
