Advertisements
Advertisements
प्रश्न
The bisectors of ∠B and ∠C of a quadrilateral ABCD intersect in P. Show that P is equidistant from the opposite sides AB and CD.
उत्तर
Given: A quadrilateral ABCD in which bisectors of ∠B and ∠C meet in P. PM ⊥ ABand PN ⊥ CD.
To prove: PM = PN
Construction: Draw PL ⊥ BC
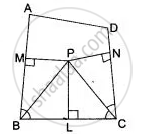
Proof: Since, P lies on the bisector of ∠B
∴ P is equidistant from BC and BA
⇒ PL = PM ...(i)
Also, P lies on the bisector of ∠C ...[Given]
∴ P is equidistant from CB and CD
⇒ PL = PN ...(ii)
From (i) and (ii), we have
PL = PM
and PL = PN
⇒ PM = PN.
Hence proved.
APPEARS IN
संबंधित प्रश्न
In triangle LMN, bisectors of interior angles at L and N intersect each other at point A. Prove that:
- Point A is equidistant from all the three sides of the triangle.
- AM bisects angle LMN.
Draw an angle ABC = 75°. Draw the locus of all the points equidistant from AB and BC.
Draw an ∠ABC = 60°, having AB = 4.6 cm and BC = 5 cm. Find a point P equidistant from AB and BC; and also equidistant from A and B.
Describe the locus of the door handle, as the door opens.
Describe the locus of points inside a circle and equidistant from two fixed points on the circumference of the circle.
In Δ ABC, the perpendicular bisector of AB and AC meet at 0. Prove that O is equidistant from the three vertices. Also, prove that if M is the mid-point of BC then OM meets BC at right angles.
In a quadrilateral ABCD, if the perpendicular bisectors of AB and AD meet at P, then prove that BP = DP.
In Fig. ABCD is a quadrilateral in which AB = BC. E is the point of intersection of the right bisectors of AD and CD. Prove that BE bisects ∠ABC.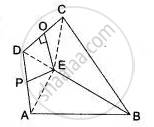
Find the locus of points which are equidistant from three non-collinear points.
ΔPBC and ΔQBC are two isosceles triangles on the same base BC but on the opposite sides of line BC. Show that PQ bisects BC at right angles.
