Advertisements
Advertisements
प्रश्न
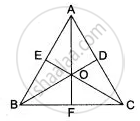
In Δ ABC, the perpendicular bisector of AB and AC meet at 0. Prove that O is equidistant from the three vertices. Also, prove that if M is the mid-point of BC then OM meets BC at right angles.
उत्तर
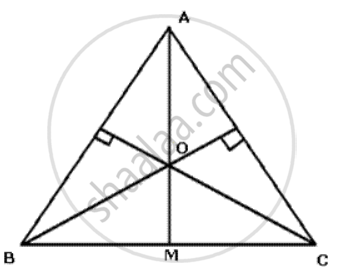
Since O lies on the perpendirular bisector of AB, O is equidistant from A and B.
OA = OB ........ (i)
Again, O lies on the perpendirular bisector of AC, O is equidistant from A and C.
OA = OC ......... (ii)
From (i) and (ii)
OB= OC
Now in Δ OBM and Δ OCM,
OB = OC (proved)
OM=OM
BM =CM ( M is mid-point of BC)
Therefore, Δ OBM and Δ OCM are congruent.
∠ OMB= ∠ OMC
But BMC is a straight line, so
∠ OMB =∠ OMC = 90°
Thus, OM meets BC at right angles.
APPEARS IN
संबंधित प्रश्न
In parallelogram ABCD, side AB is greater than side BC and P is a point in AC such that PB bisects angle B. Prove that P is equidistant from AB and BC.
Use ruler and compasses only for this question.
- Construct ΔABC, where AB = 3.5 cm, BC = 6 cm and ∠ABC = 60°.
- Construct the locus of points inside the triangle which are equidistant from BA and BC.
- Construct the locus of points inside the triangle which are equidistant from B and C.
- Mark the point P which is equidistant from AB, BC and also equidistant from B and C. Measure and record the length of PB.
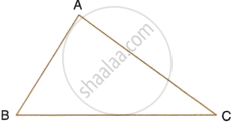
In the given triangle ABC, find a point P equidistant from AB and AC; and also equidistant from B and C.
Describe the locus of the moving end of the minute hand of a clock.
Describe the locus of a point in rhombus ABCD, so that it is equidistant from
- AB and BC;
- B and D.
A straight line AB is 8 cm long. Draw and describe the locus of a point which is:
- always 4 cm from the line AB.
- equidistant from A and B.
Mark the two points X and Y, which are 4 cm from AB and equidistant from A and B. Describe the figure AXBY.
Prove that the common chord of two intersecting circles is bisected at right angles by the line of centres.
In Fig. ABCD is a quadrilateral in which AB = BC. E is the point of intersection of the right bisectors of AD and CD. Prove that BE bisects ∠ABC.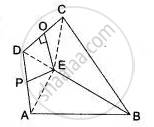
Find the locus of the centre of a circle of radius r touching externally a circle of radius R.
In Fig. AB = AC, BD and CE are the bisectors of ∠ABC and ∠ACB respectively such that BD and CE intersect each other at O. AO produced meets BC at F. Prove that AF is the right bisector of BC.