Advertisements
Advertisements
प्रश्न
Describe the locus of the moving end of the minute hand of a clock.
उत्तर
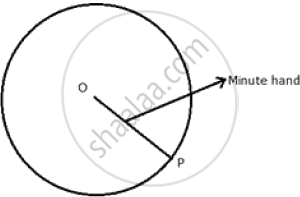
The locus of the moving end of the minute hand of the clock will be a circle where radius will be the length of the minute hand.
APPEARS IN
संबंधित प्रश्न
Construct a triangle ABC, in which AB = 4.2 cm, BC = 6.3 cm and AC = 5 cm. Draw perpendicular bisector of BC which meets AC at point D. Prove that D is equidistant from B and C.
In triangle LMN, bisectors of interior angles at L and N intersect each other at point A. Prove that:
- Point A is equidistant from all the three sides of the triangle.
- AM bisects angle LMN.
Construct a triangle ABC, with AB = 7 cm, BC = 8 cm and ∠ABC = 60°. Locate by construction the point P such that:
- P is equidistant from B and C.
- P is equidistant from AB and BC.
Measure and record the length of PB.
Describe the locus of a runner, running around a circular track and always keeping a distance of 1.5 m from the inner edge.
Describe the locus of points inside a circle and equidistant from two fixed points on the circumference of the circle.
Describe the locus of points at distances less than 3 cm from a given point.
Describe the locus of points at distances greater than 4 cm from a given point.
In Fig. ABCD is a quadrilateral in which AB = BC. E is the point of intersection of the right bisectors of AD and CD. Prove that BE bisects ∠ABC.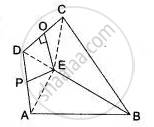
ΔPBC and ΔQBC are two isosceles triangles on the same base BC but on the opposite sides of line BC. Show that PQ bisects BC at right angles.
Given: ∠BAC, a line intersects the arms of ∠BAC in P and Q. How will you locate a point on line segment PQ, which is equidistant from AB and AC? Does such a point always exist?
