Advertisements
Advertisements
प्रश्न
In Fig. ABCD is a quadrilateral in which AB = BC. E is the point of intersection of the right bisectors of AD and CD. Prove that BE bisects ∠ABC.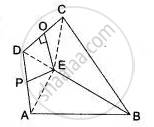
उत्तर
Given: A quadrilateral ABCD in which AB = BC. PE and QE are right bisectors or AD and CD respectively such that they meet at E.
To prove: BE bisects ∠ABC.
Construction: Join AE, DE and CE.
Proof: Since, PE is the right bisector of AD and E lies on it.
∴ AE = ED ...(i)
[∵ Points on the right bisector of a line segment are equidistant from the ends of the segment]
Also, QE is the right bisector of CD and E lies on it.
∴ ED = EC ...(ii)
From (i) and (ii), we get
AE = EC ...(iii)
Now, in Δs ABE and CBE, we have
AB = BC ...[Given]
BE = BE ...[Common]
and AE = EC ...[From (iii)]
So, by SSS criterion of congruence
ΔABE = ΔACE
⇒ ∠ABE = ∠CBE
⇒ BE bisects ∠ABC.
Hence, BE is the bisector of ∠ABC.
Hence proved.
APPEARS IN
संबंधित प्रश्न
The given figure shows a triangle ABC in which AD bisects angle BAC. EG is perpendicular bisector of side AB which intersects AD at point F.
Prove that:
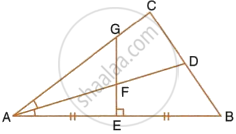
F is equidistant from AB and AC.
Draw a line AB = 6 cm. Draw the locus of all the points which are equidistant from A and B.
Describe the locus for questions 1 to 13 given below:
1. The locus of a point at a distant 3 cm from a fixed point.
Describe the locus of the centre of a wheel of a bicycle going straight along a level road.
Describe the locus of the centres of all circles passing through two fixed points.
Describe the locus of points at distances greater than 4 cm from a given point.
Describe the locus of points at distances less than or equal to 2.5 cm from a given point.
Sketch and describe the locus of the vertices of all triangles with a given base and a given altitude.
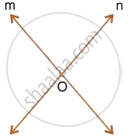
In the given figure, obtain all the points equidistant from lines m and n; and 2.5 cm from O.
Given: ∠BAC, a line intersects the arms of ∠BAC in P and Q. How will you locate a point on line segment PQ, which is equidistant from AB and AC? Does such a point always exist?
