Advertisements
Advertisements
Question
In Fig. ABCD is a quadrilateral in which AB = BC. E is the point of intersection of the right bisectors of AD and CD. Prove that BE bisects ∠ABC.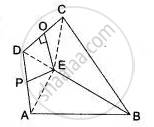
Solution
Given: A quadrilateral ABCD in which AB = BC. PE and QE are right bisectors or AD and CD respectively such that they meet at E.
To prove: BE bisects ∠ABC.
Construction: Join AE, DE and CE.
Proof: Since, PE is the right bisector of AD and E lies on it.
∴ AE = ED ...(i)
[∵ Points on the right bisector of a line segment are equidistant from the ends of the segment]
Also, QE is the right bisector of CD and E lies on it.
∴ ED = EC ...(ii)
From (i) and (ii), we get
AE = EC ...(iii)
Now, in Δs ABE and CBE, we have
AB = BC ...[Given]
BE = BE ...[Common]
and AE = EC ...[From (iii)]
So, by SSS criterion of congruence
ΔABE = ΔACE
⇒ ∠ABE = ∠CBE
⇒ BE bisects ∠ABC.
Hence, BE is the bisector of ∠ABC.
Hence proved.
APPEARS IN
RELATED QUESTIONS
In triangle LMN, bisectors of interior angles at L and N intersect each other at point A. Prove that:
- Point A is equidistant from all the three sides of the triangle.
- AM bisects angle LMN.
Describe the locus of the centre of a wheel of a bicycle going straight along a level road.
Describe the locus of the moving end of the minute hand of a clock.
The speed of sound is 332 metres per second. A gun is fired. Describe the locus of all the people on the earth’s surface, who hear the sound exactly one second later.
Find the locus of the centre of a circle of radius r touching externally a circle of radius R.
Find the locus of points which are equidistant from three non-collinear points.
ΔPBC, ΔQBC and ΔRBC are three isosceles triangles on the same base BC. Show that P, Q and R are collinear.
In Fig. AB = AC, BD and CE are the bisectors of ∠ABC and ∠ACB respectively such that BD and CE intersect each other at O. AO produced meets BC at F. Prove that AF is the right bisector of BC.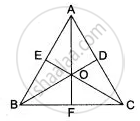
Given: ∠BAC, a line intersects the arms of ∠BAC in P and Q. How will you locate a point on line segment PQ, which is equidistant from AB and AC? Does such a point always exist?
Use ruler and compasses for the following question taking a scale of 10 m = 1 cm. A park in a city is bounded by straight fences AB, BC, CD and DA. Given that AB = 50 m, BC = 63 m, ∠ABC = 75°. D is a point equidistant from the fences AB and BC. If ∠BAD = 90°, construct the outline of the park ABCD. Also locate a point P on the line BD for the flag post which is equidistant from the corners of the park A and B.
