Advertisements
Advertisements
Question
Describe the locus of the centre of a wheel of a bicycle going straight along a level road.
Solution
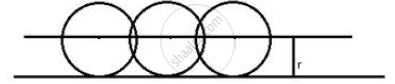
The locus of the centre of a wheel, which is going straight along a level road will be a straight line parallel to the road at a distance equal to the radius of the wheel.
APPEARS IN
RELATED QUESTIONS
In each of the given figures; PA = PB and QA = QB.
| i. | 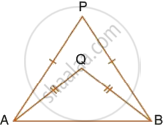 |
| ii. | 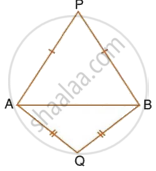 |
Prove, in each case, that PQ (produce, if required) is perpendicular bisector of AB. Hence, state the locus of the points equidistant from two given fixed points.
The given figure shows a triangle ABC in which AD bisects angle BAC. EG is perpendicular bisector of side AB which intersects AD at point F.
Prove that:
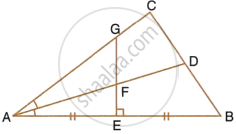
F is equidistant from A and B.
Draw a line AB = 6 cm. Draw the locus of all the points which are equidistant from A and B.
Draw an angle ABC = 75°. Draw the locus of all the points equidistant from AB and BC.
In the given triangle ABC, find a point P equidistant from AB and AC; and also equidistant from B and C.
Construct a triangle ABC, with AB = 7 cm, BC = 8 cm and ∠ABC = 60°. Locate by construction the point P such that:
- P is equidistant from B and C.
- P is equidistant from AB and BC.
Measure and record the length of PB.
Describe the locus of the door handle, as the door opens.
In a quadrilateral PQRS, if the bisectors of ∠ SPQ and ∠ PQR meet at O, prove that O is equidistant from PS and QR.
Find the locus of the centre of a circle of radius r touching externally a circle of radius R.
Given: ∠BAC, a line intersects the arms of ∠BAC in P and Q. How will you locate a point on line segment PQ, which is equidistant from AB and AC? Does such a point always exist?
