Advertisements
Advertisements
Question
The given figure shows a triangle ABC in which AD bisects angle BAC. EG is perpendicular bisector of side AB which intersects AD at point F.
Prove that:
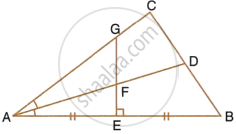
F is equidistant from A and B.
Solution

Construction: Join FB and FC
Proof: In ΔAFE and ΔFBE,
AE = EB ...(E is the mid-point of AB)
∠FEA = ∠FEB ...(Each = 90°)
FE = FE ...(Common)
∴ By side Angle side criterion of congruence,
ΔAFE ≅ ΔFBE ...(SAS Postulate)
The corresponding parts of the congruent triangles are congruent.
∴ AF = FB ...(C.P.C.T.)
Hence, F is equidistant from A and B.
APPEARS IN
RELATED QUESTIONS
In each of the given figures; PA = PB and QA = QB.
| i. | 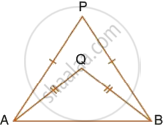 |
| ii. | 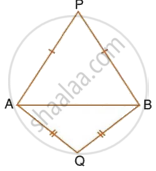 |
Prove, in each case, that PQ (produce, if required) is perpendicular bisector of AB. Hence, state the locus of the points equidistant from two given fixed points.
Use ruler and compasses only for this question.
- Construct ΔABC, where AB = 3.5 cm, BC = 6 cm and ∠ABC = 60°.
- Construct the locus of points inside the triangle which are equidistant from BA and BC.
- Construct the locus of points inside the triangle which are equidistant from B and C.
- Mark the point P which is equidistant from AB, BC and also equidistant from B and C. Measure and record the length of PB.
The given figure shows a triangle ABC in which AD bisects angle BAC. EG is perpendicular bisector of side AB which intersects AD at point F.
Prove that:
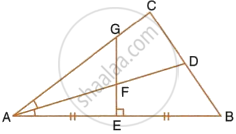
F is equidistant from AB and AC.
In the given triangle ABC, find a point P equidistant from AB and AC; and also equidistant from B and C.
Describe the locus for questions 1 to 13 given below:
1. The locus of a point at a distant 3 cm from a fixed point.
Describe the locus of the centre of a wheel of a bicycle going straight along a level road.
Describe the locus of a runner, running around a circular track and always keeping a distance of 1.5 m from the inner edge.
The speed of sound is 332 metres per second. A gun is fired. Describe the locus of all the people on the earth’s surface, who hear the sound exactly one second later.
Describe the locus of points at distances greater than or equal to 35 mm from a given point.
In the given figure, obtain all the points equidistant from lines m and n; and 2.5 cm from O.