Advertisements
Advertisements
Question
Given: ∠BAC, a line intersects the arms of ∠BAC in P and Q. How will you locate a point on line segment PQ, which is equidistant from AB and AC? Does such a point always exist?
Solution
Since, locus of points equidistant from AB and AC is the bisector of ∠BAC. Draw the bisector of ∠BAC intersecting PQ at R.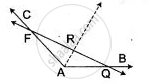
Since,R is on the bisector, so it is equidistant from AB and AC.
Yes, such a point always exists as there will be definitely a point where angular bisector and line will intersect.
Hence, R is the required point.
APPEARS IN
RELATED QUESTIONS
Construct a right angled triangle PQR, in which ∠Q = 90°, hypotenuse PR = 8 cm and QR = 4.5 cm. Draw bisector of angle PQR and let it meets PR at point T. Prove that T is equidistant from PQ and QR.
Describe the locus of the centres of all circles passing through two fixed points.
Describe the locus of points at distances less than 3 cm from a given point.
Describe the locus of points at distances greater than 4 cm from a given point.
Describe the locus of points at distances less than or equal to 2.5 cm from a given point.
In Δ ABC, the perpendicular bisector of AB and AC meet at 0. Prove that O is equidistant from the three vertices. Also, prove that if M is the mid-point of BC then OM meets BC at right angles.
In a quadrilateral ABCD, if the perpendicular bisectors of AB and AD meet at P, then prove that BP = DP.
ΔPBC and ΔQBC are two isosceles triangles on the same base. Show that the line PQ is bisector of BC and is perpendicular to BC.
ΔPBC and ΔQBC are two isosceles triangles on the same base BC but on the opposite sides of line BC. Show that PQ bisects BC at right angles.
The bisectors of ∠B and ∠C of a quadrilateral ABCD intersect in P. Show that P is equidistant from the opposite sides AB and CD.
