Advertisements
Advertisements
Question
The bisectors of ∠B and ∠C of a quadrilateral ABCD intersect in P. Show that P is equidistant from the opposite sides AB and CD.
Solution
Given: A quadrilateral ABCD in which bisectors of ∠B and ∠C meet in P. PM ⊥ ABand PN ⊥ CD.
To prove: PM = PN
Construction: Draw PL ⊥ BC
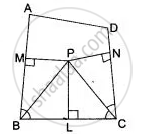
Proof: Since, P lies on the bisector of ∠B
∴ P is equidistant from BC and BA
⇒ PL = PM ...(i)
Also, P lies on the bisector of ∠C ...[Given]
∴ P is equidistant from CB and CD
⇒ PL = PN ...(ii)
From (i) and (ii), we have
PL = PM
and PL = PN
⇒ PM = PN.
Hence proved.
APPEARS IN
RELATED QUESTIONS
Describe the locus for questions 1 to 13 given below:
1. The locus of a point at a distant 3 cm from a fixed point.
Describe the locus of a stone dropped from the top of a tower.
Describe the locus of a point in rhombus ABCD, so that it is equidistant from
- AB and BC;
- B and D.
The speed of sound is 332 metres per second. A gun is fired. Describe the locus of all the people on the earth’s surface, who hear the sound exactly one second later.
A straight line AB is 8 cm long. Draw and describe the locus of a point which is:
- always 4 cm from the line AB.
- equidistant from A and B.
Mark the two points X and Y, which are 4 cm from AB and equidistant from A and B. Describe the figure AXBY.
Draw a triangle ABC in which AB = 6 cm, BC = 4.5 cm and AC = 5 cm. Draw and label:
- the locus of the centres of all circles which touch AB and AC,
- the locus of the centres of all the circles of radius 2 cm which touch AB.
Hence, construct the circle of radius 2 cm which touches AB and AC .
In Δ ABC, the perpendicular bisector of AB and AC meet at 0. Prove that O is equidistant from the three vertices. Also, prove that if M is the mid-point of BC then OM meets BC at right angles.
Prove that the common chord of two intersecting circles is bisected at right angles by the line of centres.
ΔPBC and ΔQBC are two isosceles triangles on the same base. Show that the line PQ is bisector of BC and is perpendicular to BC.
ΔPBC, ΔQBC and ΔRBC are three isosceles triangles on the same base BC. Show that P, Q and R are collinear.
