Advertisements
Advertisements
Question
ΔPBC and ΔQBC are two isosceles triangles on the same base BC but on the opposite sides of line BC. Show that PQ bisects BC at right angles.
Solution
Given: Two ΔSPBC and QBC on the same base BC but in the opposite sides of BC such that PB = PC and QB = QC.
To prove: PQ bisects BC and is ⊥ to BC.
Proof: Since, the locus of points equidistant from two given points is the perpendicular bisector of the segment joining them. Therefore, ΔPBC is isoceles
⇒ P lies on the perpendicular bisector of BC
ΔQBC is isoceles ⇒ QB = QC
⇒ Q lies on the perpendicular bisectors of BC
∴ PQ is the perpendicular bisectors of BC
Hence, PQ bisects BC at right angles.
Hence proved.
APPEARS IN
RELATED QUESTIONS
The given figure shows a triangle ABC in which AD bisects angle BAC. EG is perpendicular bisector of side AB which intersects AD at point F.
Prove that:
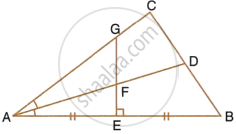
F is equidistant from A and B.
Draw an angle ABC = 75°. Draw the locus of all the points equidistant from AB and BC.
Draw an ∠ABC = 60°, having AB = 4.6 cm and BC = 5 cm. Find a point P equidistant from AB and BC; and also equidistant from A and B.
Describe the locus of a runner, running around a circular track and always keeping a distance of 1.5 m from the inner edge.
Describe the locus of points at distances greater than 4 cm from a given point.
Sketch and describe the locus of the vertices of all triangles with a given base and a given altitude.
By actual drawing obtain the points equidistant from lines m and n; and 6 cm from a point P, where P is 2 cm above m, m is parallel to n and m is 6 cm above n.
Prove that the common chord of two intersecting circles is bisected at right angles by the line of centres.
Find the locus of the centre of a circle of radius r touching externally a circle of radius R.
Given: ∠BAC, a line intersects the arms of ∠BAC in P and Q. How will you locate a point on line segment PQ, which is equidistant from AB and AC? Does such a point always exist?
