Advertisements
Advertisements
Question
Draw a line AB = 6 cm. Draw the locus of all the points which are equidistant from A and B.
Solution
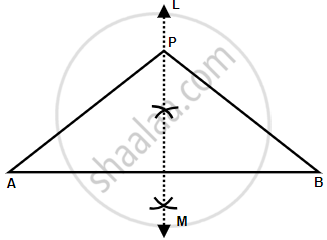
Steps of construction:
- Draw a line segment AB of 6 cm.
- Draw perpendicular bisector LM of AB. LM is the required locus.
- Take any point on LM say P.
- Join PA and PB. Since, P lies on the right bisector of line AB.
Therefore, P is equidistant from A and B.
i.e. PA = PB
Hence, Perpendicular bisector of AB is the locus of all points which are equidistant from A and B.
APPEARS IN
RELATED QUESTIONS
In each of the given figures; PA = PB and QA = QB.
| i. | 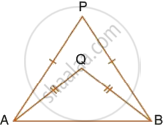 |
| ii. | 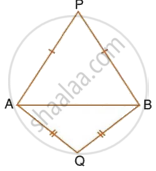 |
Prove, in each case, that PQ (produce, if required) is perpendicular bisector of AB. Hence, state the locus of the points equidistant from two given fixed points.
In the figure given below, find a point P on CD equidistant from points A and B.

Describe the locus of points at a distance 2 cm from a fixed line.
Describe the locus of the moving end of the minute hand of a clock.
Describe the locus of a stone dropped from the top of a tower.
Describe the locus of points inside a circle and equidistant from two fixed points on the circumference of the circle.
Describe the locus of points at distances less than or equal to 2.5 cm from a given point.
In a quadrilateral ABCD, if the perpendicular bisectors of AB and AD meet at P, then prove that BP = DP.
Find the locus of points which are equidistant from three non-collinear points.
ΔPBC, ΔQBC and ΔRBC are three isosceles triangles on the same base BC. Show that P, Q and R are collinear.
