Advertisements
Advertisements
Question
Describe the locus of points inside a circle and equidistant from two fixed points on the circumference of the circle.
Solution
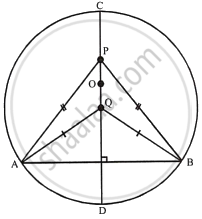
The locus of the points inside the circle which are equidistant from the fixed points on the circumference of a circle will be the diameter which is perpendicular bisector of the line joining the two fixed points on the circle.
APPEARS IN
RELATED QUESTIONS
Construct a triangle ABC, in which AB = 4.2 cm, BC = 6.3 cm and AC = 5 cm. Draw perpendicular bisector of BC which meets AC at point D. Prove that D is equidistant from B and C.
Construct a right angled triangle PQR, in which ∠Q = 90°, hypotenuse PR = 8 cm and QR = 4.5 cm. Draw bisector of angle PQR and let it meets PR at point T. Prove that T is equidistant from PQ and QR.
Draw an ∠ABC = 60°, having AB = 4.6 cm and BC = 5 cm. Find a point P equidistant from AB and BC; and also equidistant from A and B.
Describe the locus of the centre of a wheel of a bicycle going straight along a level road.
Describe the locus of a point in rhombus ABCD, so that it is equidistant from
- AB and BC;
- B and D.
The speed of sound is 332 metres per second. A gun is fired. Describe the locus of all the people on the earth’s surface, who hear the sound exactly one second later.
In Δ ABC, the perpendicular bisector of AB and AC meet at 0. Prove that O is equidistant from the three vertices. Also, prove that if M is the mid-point of BC then OM meets BC at right angles.
In a quadrilateral ABCD, if the perpendicular bisectors of AB and AD meet at P, then prove that BP = DP.
Find the locus of the centre of a circle of radius r touching externally a circle of radius R.
Show that the locus of the centres of all circles passing through two given points A and B, is the perpendicular bisector of the line segment AB.
