Advertisements
Advertisements
प्रश्न
Describe the locus of points inside a circle and equidistant from two fixed points on the circumference of the circle.
उत्तर
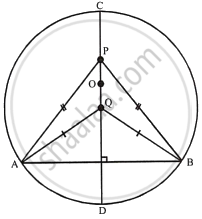
The locus of the points inside the circle which are equidistant from the fixed points on the circumference of a circle will be the diameter which is perpendicular bisector of the line joining the two fixed points on the circle.
APPEARS IN
संबंधित प्रश्न
Construct a right angled triangle PQR, in which ∠Q = 90°, hypotenuse PR = 8 cm and QR = 4.5 cm. Draw bisector of angle PQR and let it meets PR at point T. Prove that T is equidistant from PQ and QR.
Use ruler and compasses only for this question.
- Construct ΔABC, where AB = 3.5 cm, BC = 6 cm and ∠ABC = 60°.
- Construct the locus of points inside the triangle which are equidistant from BA and BC.
- Construct the locus of points inside the triangle which are equidistant from B and C.
- Mark the point P which is equidistant from AB, BC and also equidistant from B and C. Measure and record the length of PB.
Draw a line AB = 6 cm. Draw the locus of all the points which are equidistant from A and B.
Draw an ∠ABC = 60°, having AB = 4.6 cm and BC = 5 cm. Find a point P equidistant from AB and BC; and also equidistant from A and B.
Describe the locus of the moving end of the minute hand of a clock.
Describe the locus of points at distances less than or equal to 2.5 cm from a given point.
Describe the locus of points at distances greater than or equal to 35 mm from a given point.
By actual drawing obtain the points equidistant from lines m and n; and 6 cm from a point P, where P is 2 cm above m, m is parallel to n and m is 6 cm above n.
In a quadrilateral ABCD, if the perpendicular bisectors of AB and AD meet at P, then prove that BP = DP.
Show that the locus of the centres of all circles passing through two given points A and B, is the perpendicular bisector of the line segment AB.
