Advertisements
Advertisements
प्रश्न
Draw a line AB = 6 cm. Draw the locus of all the points which are equidistant from A and B.
उत्तर
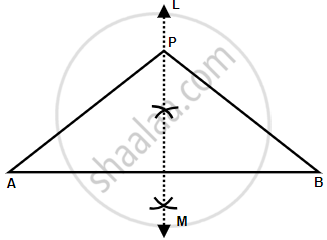
Steps of construction:
- Draw a line segment AB of 6 cm.
- Draw perpendicular bisector LM of AB. LM is the required locus.
- Take any point on LM say P.
- Join PA and PB. Since, P lies on the right bisector of line AB.
Therefore, P is equidistant from A and B.
i.e. PA = PB
Hence, Perpendicular bisector of AB is the locus of all points which are equidistant from A and B.
APPEARS IN
संबंधित प्रश्न
In parallelogram ABCD, side AB is greater than side BC and P is a point in AC such that PB bisects angle B. Prove that P is equidistant from AB and BC.
The given figure shows a triangle ABC in which AD bisects angle BAC. EG is perpendicular bisector of side AB which intersects AD at point F.
Prove that:
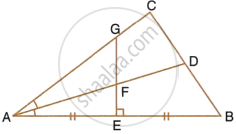
F is equidistant from A and B.
The given figure shows a triangle ABC in which AD bisects angle BAC. EG is perpendicular bisector of side AB which intersects AD at point F.
Prove that:
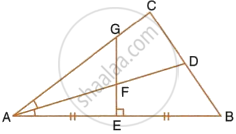
F is equidistant from AB and AC.
In the figure given below, find a point P on CD equidistant from points A and B.

Construct a triangle ABC, with AB = 7 cm, BC = 8 cm and ∠ABC = 60°. Locate by construction the point P such that:
- P is equidistant from B and C.
- P is equidistant from AB and BC.
Measure and record the length of PB.
Describe the locus of points at a distance 2 cm from a fixed line.
Describe the locus of points at distances less than or equal to 2.5 cm from a given point.
A straight line AB is 8 cm long. Draw and describe the locus of a point which is:
- always 4 cm from the line AB.
- equidistant from A and B.
Mark the two points X and Y, which are 4 cm from AB and equidistant from A and B. Describe the figure AXBY.
In Δ ABC, the perpendicular bisector of AB and AC meet at 0. Prove that O is equidistant from the three vertices. Also, prove that if M is the mid-point of BC then OM meets BC at right angles.
The bisectors of ∠B and ∠C of a quadrilateral ABCD intersect in P. Show that P is equidistant from the opposite sides AB and CD.
