Advertisements
Advertisements
प्रश्न
Draw an angle ABC = 75°. Draw the locus of all the points equidistant from AB and BC.
उत्तर
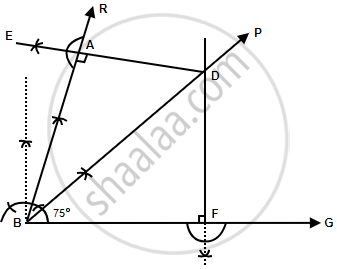
Steps of construction:
- Draw a ray BC.
- Construct a ray RA making an angle of 75° with BC. Therefore, ABC = ABC = 75°
- Draw the angle bisector BP of ∠ABC.
BP is the required locus. - Take any point D on BP.
- From D, draw DE ⊥ AB and DF ⊥ BC.
Since D lies on the angle bisector BP of ∠ABC.
D is equidistant from AB and BC.
Hence, DE = DF
Similarly, any point on BP is equidistant from AB and BC.
Therefore, BP is the locus of all points which are equidistant from AB and BC.
APPEARS IN
संबंधित प्रश्न
Describe the locus for questions 1 to 13 given below:
1. The locus of a point at a distant 3 cm from a fixed point.
Describe the locus of points inside a circle and equidistant from two fixed points on the circumference of the circle.
Describe the locus of the centres of all circles passing through two fixed points.
Describe the locus of a point in rhombus ABCD, so that it is equidistant from
- AB and BC;
- B and D.
The speed of sound is 332 metres per second. A gun is fired. Describe the locus of all the people on the earth’s surface, who hear the sound exactly one second later.
Describe the locus of points at distances greater than 4 cm from a given point.
Sketch and describe the locus of the vertices of all triangles with a given base and a given altitude.
In a quadrilateral PQRS, if the bisectors of ∠ SPQ and ∠ PQR meet at O, prove that O is equidistant from PS and QR.
Find the locus of points which are equidistant from three non-collinear points.
ΔPBC, ΔQBC and ΔRBC are three isosceles triangles on the same base BC. Show that P, Q and R are collinear.
