Advertisements
Advertisements
प्रश्न
Show that the locus of the centres of all circles passing through two given points A and B, is the perpendicular bisector of the line segment AB.
उत्तर
Let P and Q be the centres of two circles S and S', each passing through two given points A and B. Then,
PA = PB ...[Radii of the same circle]
⇒ P lies on the perpendicular bisector of AB ...(i)
Again, QA = QB ...[Radii of the same circle]
⇒ Q lies on the perpendicular bisector of AB ...(ii)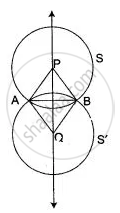
From (i) and (ii), it follows that P and Q both lies on the perpendicular bisector of AB.
Hence, the locus of the centres of all the circles passing through A and B is the perpendicular bisector of AB.
APPEARS IN
संबंधित प्रश्न
Use ruler and compasses only for this question.
- Construct ΔABC, where AB = 3.5 cm, BC = 6 cm and ∠ABC = 60°.
- Construct the locus of points inside the triangle which are equidistant from BA and BC.
- Construct the locus of points inside the triangle which are equidistant from B and C.
- Mark the point P which is equidistant from AB, BC and also equidistant from B and C. Measure and record the length of PB.
Describe the locus for questions 1 to 13 given below:
1. The locus of a point at a distant 3 cm from a fixed point.
Describe the locus of the door handle, as the door opens.
Describe the locus of points inside a circle and equidistant from two fixed points on the circumference of the circle.
Describe the locus of the centres of all circles passing through two fixed points.
Describe the locus of a point in rhombus ABCD, so that it is equidistant from
- AB and BC;
- B and D.
A straight line AB is 8 cm long. Draw and describe the locus of a point which is:
- always 4 cm from the line AB.
- equidistant from A and B.
Mark the two points X and Y, which are 4 cm from AB and equidistant from A and B. Describe the figure AXBY.
Draw a triangle ABC in which AB = 6 cm, BC = 4.5 cm and AC = 5 cm. Draw and label:
- the locus of the centres of all circles which touch AB and AC,
- the locus of the centres of all the circles of radius 2 cm which touch AB.
Hence, construct the circle of radius 2 cm which touches AB and AC .
Prove that the common chord of two intersecting circles is bisected at right angles by the line of centres.
Find the locus of the centre of a circle of radius r touching externally a circle of radius R.
