Advertisements
Advertisements
Question
Find the locus of points which are equidistant from three non-collinear points.
Solution
Let A, B and C be three non-collinear points. Join AB and BC. Let P be a moving point. Since, P is equidistant from A and B, it follows that P lies on the perpendicular bisector of AB.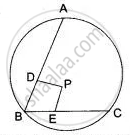
Again P is equidistant from B and C. So, P lies on the perpendicular bisector of BC.
Thus, P is the point of intersection of the perpendicular bisector of AB and BC. So, P coincides three given non-collinear points. Hence, the required locus is the centre of the circle passing through three given non-collinear points.
APPEARS IN
RELATED QUESTIONS
In parallelogram ABCD, side AB is greater than side BC and P is a point in AC such that PB bisects angle B. Prove that P is equidistant from AB and BC.
Draw an angle ABC = 75°. Draw the locus of all the points equidistant from AB and BC.
Construct a triangle ABC, with AB = 7 cm, BC = 8 cm and ∠ABC = 60°. Locate by construction the point P such that:
- P is equidistant from B and C.
- P is equidistant from AB and BC.
Measure and record the length of PB.
Describe the locus for questions 1 to 13 given below:
1. The locus of a point at a distant 3 cm from a fixed point.
Describe the locus of the moving end of the minute hand of a clock.
Describe the locus of points at distances greater than 4 cm from a given point.
Describe the locus of points at distances greater than or equal to 35 mm from a given point.
Sketch and describe the locus of the vertices of all triangles with a given base and a given altitude.
A straight line AB is 8 cm long. Draw and describe the locus of a point which is:
- always 4 cm from the line AB.
- equidistant from A and B.
Mark the two points X and Y, which are 4 cm from AB and equidistant from A and B. Describe the figure AXBY.
ΔPBC, ΔQBC and ΔRBC are three isosceles triangles on the same base BC. Show that P, Q and R are collinear.
