Advertisements
Advertisements
Question
In parallelogram ABCD, side AB is greater than side BC and P is a point in AC such that PB bisects angle B. Prove that P is equidistant from AB and BC.
Solution
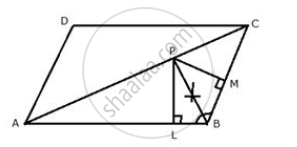
Construction: From P, draw PL ⊥ AB and PM ⊥ BC
Proof: In ΔPLB and ΔPMB
∠PLB = ∠PMB ...(Each = 90°)
∠PBL = ∠PBM ...(Given)
PB = PB ...(Common)
∴ By Angle – angle side criterion of congruence,
ΔPLB ≅ ΔPMB ...(AAS postulate)
The corresponding parts of the congruent triangles are congruent
∴ PL = PM ...(C.P.C.T.)
Hence, P is equidistant from AB and BC
APPEARS IN
RELATED QUESTIONS
Construct a right angled triangle PQR, in which ∠Q = 90°, hypotenuse PR = 8 cm and QR = 4.5 cm. Draw bisector of angle PQR and let it meets PR at point T. Prove that T is equidistant from PQ and QR.
Construct a triangle ABC, with AB = 7 cm, BC = 8 cm and ∠ABC = 60°. Locate by construction the point P such that:
- P is equidistant from B and C.
- P is equidistant from AB and BC.
Measure and record the length of PB.
Describe the locus of the centre of a wheel of a bicycle going straight along a level road.
Describe the locus of a runner, running around a circular track and always keeping a distance of 1.5 m from the inner edge.
Describe the locus of points at distances less than 3 cm from a given point.
Describe the locus of points at distances less than or equal to 2.5 cm from a given point.
By actual drawing obtain the points equidistant from lines m and n; and 6 cm from a point P, where P is 2 cm above m, m is parallel to n and m is 6 cm above n.
In a quadrilateral ABCD, if the perpendicular bisectors of AB and AD meet at P, then prove that BP = DP.
Find the locus of points which are equidistant from three non-collinear points.
Use ruler and compasses for the following question taking a scale of 10 m = 1 cm. A park in a city is bounded by straight fences AB, BC, CD and DA. Given that AB = 50 m, BC = 63 m, ∠ABC = 75°. D is a point equidistant from the fences AB and BC. If ∠BAD = 90°, construct the outline of the park ABCD. Also locate a point P on the line BD for the flag post which is equidistant from the corners of the park A and B.
