Advertisements
Advertisements
प्रश्न
In parallelogram ABCD, side AB is greater than side BC and P is a point in AC such that PB bisects angle B. Prove that P is equidistant from AB and BC.
उत्तर
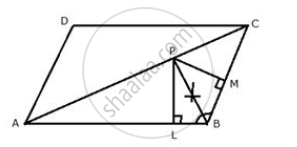
Construction: From P, draw PL ⊥ AB and PM ⊥ BC
Proof: In ΔPLB and ΔPMB
∠PLB = ∠PMB ...(Each = 90°)
∠PBL = ∠PBM ...(Given)
PB = PB ...(Common)
∴ By Angle – angle side criterion of congruence,
ΔPLB ≅ ΔPMB ...(AAS postulate)
The corresponding parts of the congruent triangles are congruent
∴ PL = PM ...(C.P.C.T.)
Hence, P is equidistant from AB and BC
APPEARS IN
संबंधित प्रश्न
In each of the given figures; PA = PB and QA = QB.
| i. | 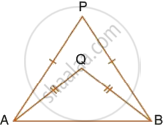 |
| ii. | 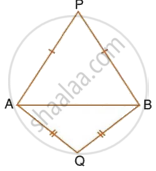 |
Prove, in each case, that PQ (produce, if required) is perpendicular bisector of AB. Hence, state the locus of the points equidistant from two given fixed points.
The given figure shows a triangle ABC in which AD bisects angle BAC. EG is perpendicular bisector of side AB which intersects AD at point F.
Prove that:
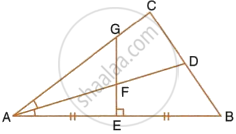
F is equidistant from AB and AC.
Draw a line AB = 6 cm. Draw the locus of all the points which are equidistant from A and B.
In the figure given below, find a point P on CD equidistant from points A and B.

Describe the locus of the centre of a wheel of a bicycle going straight along a level road.
Describe the locus of the door handle, as the door opens.
Describe the locus of points inside a circle and equidistant from two fixed points on the circumference of the circle.
Describe the locus of a point in rhombus ABCD, so that it is equidistant from
- AB and BC;
- B and D.
Find the locus of the centre of a circle of radius r touching externally a circle of radius R.
ΔPBC and ΔQBC are two isosceles triangles on the same base. Show that the line PQ is bisector of BC and is perpendicular to BC.
