Advertisements
Advertisements
प्रश्न
Describe the locus of the door handle, as the door opens.
उत्तर
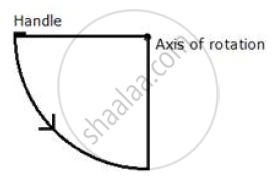
The locus of the door handle will be the circumference of a circle with centre at the axis of rotation of the door and radius equal to the distance between the door handle and the axis of rotation of the door.
APPEARS IN
संबंधित प्रश्न
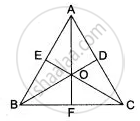
The given figure shows a triangle ABC in which AD bisects angle BAC. EG is perpendicular bisector of side AB which intersects AD at point F.
Prove that:
F is equidistant from A and B.
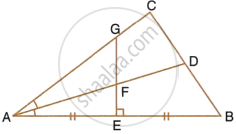
The given figure shows a triangle ABC in which AD bisects angle BAC. EG is perpendicular bisector of side AB which intersects AD at point F.
Prove that:
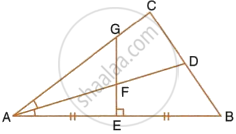
F is equidistant from AB and AC.
Draw an ∠ABC = 60°, having AB = 4.6 cm and BC = 5 cm. Find a point P equidistant from AB and BC; and also equidistant from A and B.
Describe the locus of the moving end of the minute hand of a clock.
Draw a triangle ABC in which AB = 6 cm, BC = 4.5 cm and AC = 5 cm. Draw and label:
- the locus of the centres of all circles which touch AB and AC,
- the locus of the centres of all the circles of radius 2 cm which touch AB.
Hence, construct the circle of radius 2 cm which touches AB and AC .
In Δ ABC, the perpendicular bisector of AB and AC meet at 0. Prove that O is equidistant from the three vertices. Also, prove that if M is the mid-point of BC then OM meets BC at right angles.
Prove that the common chord of two intersecting circles is bisected at right angles by the line of centres.
In Fig. ABCD is a quadrilateral in which AB = BC. E is the point of intersection of the right bisectors of AD and CD. Prove that BE bisects ∠ABC.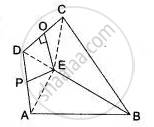
Show that the locus of the centres of all circles passing through two given points A and B, is the perpendicular bisector of the line segment AB.
In Fig. AB = AC, BD and CE are the bisectors of ∠ABC and ∠ACB respectively such that BD and CE intersect each other at O. AO produced meets BC at F. Prove that AF is the right bisector of BC.