Advertisements
Advertisements
प्रश्न
Describe the locus of the moving end of the minute hand of a clock.
उत्तर
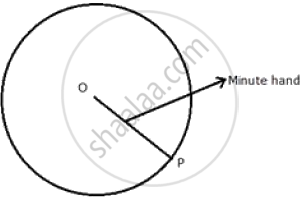
The locus of the moving end of the minute hand of the clock will be a circle where radius will be the length of the minute hand.
APPEARS IN
संबंधित प्रश्न
Construct a right angled triangle PQR, in which ∠Q = 90°, hypotenuse PR = 8 cm and QR = 4.5 cm. Draw bisector of angle PQR and let it meets PR at point T. Prove that T is equidistant from PQ and QR.
Use ruler and compasses only for this question.
- Construct ΔABC, where AB = 3.5 cm, BC = 6 cm and ∠ABC = 60°.
- Construct the locus of points inside the triangle which are equidistant from BA and BC.
- Construct the locus of points inside the triangle which are equidistant from B and C.
- Mark the point P which is equidistant from AB, BC and also equidistant from B and C. Measure and record the length of PB.
The given figure shows a triangle ABC in which AD bisects angle BAC. EG is perpendicular bisector of side AB which intersects AD at point F.
Prove that:
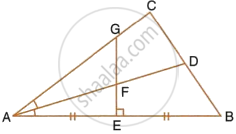
F is equidistant from AB and AC.
Draw an ∠ABC = 60°, having AB = 4.6 cm and BC = 5 cm. Find a point P equidistant from AB and BC; and also equidistant from A and B.
In the figure given below, find a point P on CD equidistant from points A and B.

Describe the locus of a runner, running around a circular track and always keeping a distance of 1.5 m from the inner edge.
In Δ ABC, the perpendicular bisector of AB and AC meet at 0. Prove that O is equidistant from the three vertices. Also, prove that if M is the mid-point of BC then OM meets BC at right angles.
Find the locus of the centre of a circle of radius r touching externally a circle of radius R.
ΔPBC and ΔQBC are two isosceles triangles on the same base BC but on the opposite sides of line BC. Show that PQ bisects BC at right angles.
Given: ∠BAC, a line intersects the arms of ∠BAC in P and Q. How will you locate a point on line segment PQ, which is equidistant from AB and AC? Does such a point always exist?
