Advertisements
Advertisements
प्रश्न
In Δ ABC, the perpendicular bisector of AB and AC meet at 0. Prove that O is equidistant from the three vertices. Also, prove that if M is the mid-point of BC then OM meets BC at right angles.
उत्तर
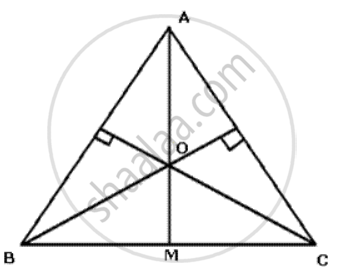
Since O lies on the perpendirular bisector of AB, O is equidistant from A and B.
OA = OB ........ (i)
Again, O lies on the perpendirular bisector of AC, O is equidistant from A and C.
OA = OC ......... (ii)
From (i) and (ii)
OB= OC
Now in Δ OBM and Δ OCM,
OB = OC (proved)
OM=OM
BM =CM ( M is mid-point of BC)
Therefore, Δ OBM and Δ OCM are congruent.
∠ OMB= ∠ OMC
But BMC is a straight line, so
∠ OMB =∠ OMC = 90°
Thus, OM meets BC at right angles.
APPEARS IN
संबंधित प्रश्न
In parallelogram ABCD, side AB is greater than side BC and P is a point in AC such that PB bisects angle B. Prove that P is equidistant from AB and BC.
The given figure shows a triangle ABC in which AD bisects angle BAC. EG is perpendicular bisector of side AB which intersects AD at point F.
Prove that:
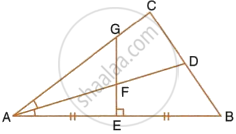
F is equidistant from AB and AC.
Draw an angle ABC = 75°. Draw the locus of all the points equidistant from AB and BC.
Describe the locus of a runner, running around a circular track and always keeping a distance of 1.5 m from the inner edge.
Describe the locus of points at distances greater than or equal to 35 mm from a given point.
Sketch and describe the locus of the vertices of all triangles with a given base and a given altitude.
In a quadrilateral PQRS, if the bisectors of ∠ SPQ and ∠ PQR meet at O, prove that O is equidistant from PS and QR.
Find the locus of the centre of a circle of radius r touching externally a circle of radius R.
ΔPBC and ΔQBC are two isosceles triangles on the same base BC but on the opposite sides of line BC. Show that PQ bisects BC at right angles.
The bisectors of ∠B and ∠C of a quadrilateral ABCD intersect in P. Show that P is equidistant from the opposite sides AB and CD.
