Advertisements
Advertisements
प्रश्न
Find the locus of points which are equidistant from three non-collinear points.
उत्तर
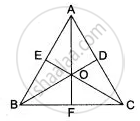
Let A, B and C be three non-collinear points. Join AB and BC. Let P be a moving point. Since, P is equidistant from A and B, it follows that P lies on the perpendicular bisector of AB.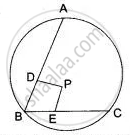
Again P is equidistant from B and C. So, P lies on the perpendicular bisector of BC.
Thus, P is the point of intersection of the perpendicular bisector of AB and BC. So, P coincides three given non-collinear points. Hence, the required locus is the centre of the circle passing through three given non-collinear points.
APPEARS IN
संबंधित प्रश्न
Construct a triangle ABC, in which AB = 4.2 cm, BC = 6.3 cm and AC = 5 cm. Draw perpendicular bisector of BC which meets AC at point D. Prove that D is equidistant from B and C.
In triangle LMN, bisectors of interior angles at L and N intersect each other at point A. Prove that:
- Point A is equidistant from all the three sides of the triangle.
- AM bisects angle LMN.
Draw a line AB = 6 cm. Draw the locus of all the points which are equidistant from A and B.
The speed of sound is 332 metres per second. A gun is fired. Describe the locus of all the people on the earth’s surface, who hear the sound exactly one second later.
Describe the locus of points at distances greater than 4 cm from a given point.
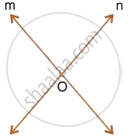
In the given figure, obtain all the points equidistant from lines m and n; and 2.5 cm from O.
Prove that the common chord of two intersecting circles is bisected at right angles by the line of centres.
Show that the locus of the centres of all circles passing through two given points A and B, is the perpendicular bisector of the line segment AB.
ΔPBC, ΔQBC and ΔRBC are three isosceles triangles on the same base BC. Show that P, Q and R are collinear.
In Fig. AB = AC, BD and CE are the bisectors of ∠ABC and ∠ACB respectively such that BD and CE intersect each other at O. AO produced meets BC at F. Prove that AF is the right bisector of BC.