Advertisements
Advertisements
प्रश्न
What is the locus of points which are equidistant from the given non-collinear point A, B and C? Justify your answer.
उत्तर
Let A, B, C be three distinct points on a line1. Any point equidistant from A and B lies on the perpendicular bisector of Ab. So, points equidistant from A and B lies on line m.
Similarly, points equidistant from B and C lies on line n which is the perpendicular bisector of BC.
Thus, any point equidistant from A, B and C must be common to both the lines m and n.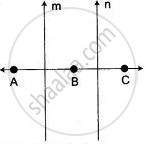
But m ⊥ AB and n ⊥ BC.
∴ m ⊥ AC and n ⊥ AC
⇒ m || n
So, no points is common to both m and n.
Hence, the required locus is the null set Φ.
APPEARS IN
संबंधित प्रश्न
Use ruler and compasses only for the following questions. All constructions lines and arcs must be clearly shown.
Construct the locus of points at a distance of 3.5 cm from A.
Use ruler and compasses only for the following questions. All constructions lines and arcs must be clearly shown
Construct the locus of points equidistant from AC and BC.
Use ruler and compasses only for the following questions. All constructions lines and arcs must be clearly shown
Mark 2 points X and Y which are a distance of 3.5 cm from A and also equidistant from AC and BC. Measure XY.
A point moves such that its distance from a fixed line AB is always the same. What is the relation between AB and the path travelled by the point?
State the locus of a point moving so that its perpendicular distances from two given lines is always equal.
AB is a fixed line) state the locus of the point P such that ∠ APB = 90° .
The bisector of ∠ B and ∠C of a quadrilateral ABCD intersect in P, show that P is equidistant from the opposite sides AB and CD.
l is the perpendicular bisector of line segment PQ and R is a point on the same side of l as P. The segment QR intersects l at X. Prove that PX + XR = QR.
Given a Δ ABC with unequal sides. Find a point which is equidistant from B and C as well as from AB and AC.
The diagonals of a quadrilateral bisect each other at right angles. Show that the quadrilateral is a rhombus.
