Advertisements
Advertisements
प्रश्न
In the given figure, obtain all the points equidistant from lines m and n; and 2.5 cm from O.
उत्तर
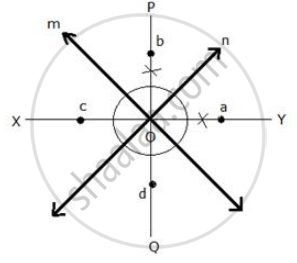
Draw an angle bisector PQ and XY of angles formed by the lines m and n.
From O, draw arcs with radius 2.5 cm, which intersect the angle bisectors at a, b, c and d respectively.
Hence, a, b, c and d are the required four points.
APPEARS IN
संबंधित प्रश्न
Construct a triangle ABC, in which AB = 4.2 cm, BC = 6.3 cm and AC = 5 cm. Draw perpendicular bisector of BC which meets AC at point D. Prove that D is equidistant from B and C.
In each of the given figures; PA = PB and QA = QB.
| i. | 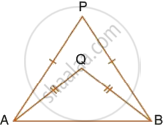 |
| ii. | 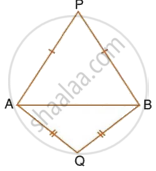 |
Prove, in each case, that PQ (produce, if required) is perpendicular bisector of AB. Hence, state the locus of the points equidistant from two given fixed points.
In triangle LMN, bisectors of interior angles at L and N intersect each other at point A. Prove that:
- Point A is equidistant from all the three sides of the triangle.
- AM bisects angle LMN.
Draw an ∠ABC = 60°, having AB = 4.6 cm and BC = 5 cm. Find a point P equidistant from AB and BC; and also equidistant from A and B.
Describe the locus of a stone dropped from the top of a tower.
Describe the locus of the centres of all circles passing through two fixed points.
Describe the locus of points at distances less than 3 cm from a given point.
Describe the locus of points at distances greater than 4 cm from a given point.
In Δ ABC, the perpendicular bisector of AB and AC meet at 0. Prove that O is equidistant from the three vertices. Also, prove that if M is the mid-point of BC then OM meets BC at right angles.
ΔPBC and ΔQBC are two isosceles triangles on the same base. Show that the line PQ is bisector of BC and is perpendicular to BC.
