Advertisements
Advertisements
Questions
Without using set squares or protractor, construct a quadrilateral ABCD in which ∠ BAD = 45° , AD = AB = 6 cm, BC= 3.6 cm and CD=5 cm. Locate the point P on BD which is equidistant from BC and CD.
Without using set squares or protractor, construct a quadrilateral ABCD in which ∠ BAD = 45° , AD = AB = 6 cm, BC= 3.6 cm and CD=5 cm.
(i) Measure ∠BCD
(ii) Locate point P on BD which is equidistant from BC and CD.
Solution 1
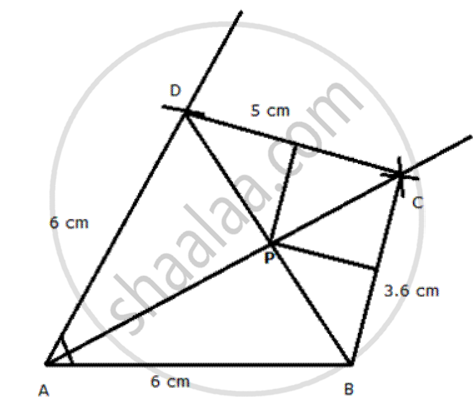
Steps of construction:
(i) Draw a line AB = 6 cm.
(ii) Draw a ray making an angle of 45° with AB.
(iii) With a as centre, draw AD = 6 cm on the ray.
(iv) Draw an angle bisector of angle BAD.
(v) With Bas centre cut an arc BC = 3.6 cm on the angle bisector.
(vi) With Das centre cut an arc CD = 5 cm on the angle bisector. ABCD is the required quadrilateral.
(vii) Join BD.
(viii) Draw perpendicular bisectors of CD and BC which meet BD on P. Pis the required point.
Solution 2
(i) ∠BCD = 62°.
(ii) Draw angle bisector of ∠BCD. Join BD.
The point on intersection of the bisector and BD is P. P is equidistant from BC and CD.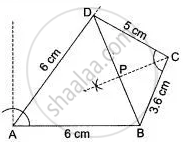
APPEARS IN
RELATED QUESTIONS
Construct a triangle ABC, with AB = 5.6 cm, AC = BC = 9.2 cm. Find the points equidistant from AB and AC; and also 2 cm from BC. Measure the distance between the two points obtained.
Construct a triangle BCP given BC = 5 cm, BP = 4 cm and ∠PBC = 45°.
- Complete the rectangle ABCD such that:
- P is equidistant from AB and BC.
- P is equidistant from C and D.
- Measure and record the length of AB.
Construct a ti.PQR, in which PQ=S. 5 cm, QR=3. 2 cm and PR=4.8 cm. Draw the locus of a point which moves so that it is always 2.5 cm from Q.
Construct a Δ XYZ in which XY= 4 cm, YZ = 5 cm and ∠ Y = 1200. Locate a point T such that ∠ YXT is a right angle and Tis equidistant from Y and Z. Measure TZ.
Describe completely the locus of point in the following cases:
Midpoint of radii of a circle.
Describe completely the locus of points in the following cases:
Centre of a cirde of radius 2 cm and touching a fixed circle of radius 3 cm with centre O.
Draw and describe the locus in the following cases :
The locus of a point in the rhombus ABCD which is equidistant from the point A and C
Use ruler and compass only for the following question. All construction lines and arcs must be clearly shown.
- Construct a ΔABC in which BC = 6.5 cm, ∠ABC = 60°, AB = 5 cm.
- Construct the locus of points at a distance of 3.5 cm from A.
- Construct the locus of points equidistant from AC and BC.
- Mark 2 points X and Y which are at a distance of 3.5 cm from A and also equidistant from AC and BC. Measure XY.
Without using set squares or protractor construct a triangle ABC in which AB = 4 cm, BC = 5 cm and ∠ABC = 120°.
(i) Locate the point P such that ∠BAp = 90° and BP = CP.
(ii) Measure the length of BP.
Use ruler and compasses only for the following questions:
Construct triangle BCP, when CB = 5 cm, BP = 4 cm, ∠PBC = 45°.
Complete the rectangle ABCD such that :
(i) P is equidistant from AB and BC and
(ii) P is equidistant from C and D. Measure and write down the length of AB.
