Advertisements
Advertisements
Question
Draw and describe the locus in the following cases :
The locus of a point in the rhombus ABCD which is equidistant from the point A and C
Solution
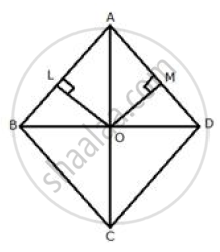
Diagonal AC and BD bisect each other at right angles at O.
Hence, O is equidistant from A and C.
APPEARS IN
RELATED QUESTIONS
Construct a triangle ABC, with AB = 5.6 cm, AC = BC = 9.2 cm. Find the points equidistant from AB and AC; and also 2 cm from BC. Measure the distance between the two points obtained.
Ruler and compasses may be used in this question. All construction lines and arcs must be clearly shown and be of sufficient length and clarity to permit assessment.
- Construct a ΔABC, in which BC = 6 cm, AB = 9 cm and angle ABC = 60°.
- Construct the locus of all points inside triangle ABC, which are equidistant from B and C.
- Construct the locus of the vertices of the triangles with BC as base and which are equal in area to triangle ABC.
- Mark the point Q, in your construction, which would make ΔQBC equal in area to ΔABC, and isosceles.
- Measure and record the length of CQ.
Construct a triangle BCP given BC = 5 cm, BP = 4 cm and ∠PBC = 45°.
- Complete the rectangle ABCD such that:
- P is equidistant from AB and BC.
- P is equidistant from C and D.
- Measure and record the length of AB.
Two straight roads AB and CD cross each other at Pat an angle of 75° . X is a stone on the road AB, 800m from P towards B. BY taking an appropriate scale draw a figure to locate the position of a pole, which is equidistant from P and X, and is also equidistant from the roads.
Without using set squares or protractor, construct a quadrilateral ABCD in which ∠ BAD = 45° , AD = AB = 6 cm, BC= 3.6 cm and CD=5 cm. Locate the point P on BD which is equidistant from BC and CD.
Construct a rhombus ABCD with sides of length 5 cm and diagonal AC of length 6 cm. Measure ∠ ABC. Find the point R on AD such that RB = RC. Measure the length of AR.
In Δ PQR, s is a point on PR such that ∠ PQS = ∠ RQS . Prove thats is equidistant from PQ and QR.
A and B are fixed points while Pis a moving point, moving in a way that it is always equidistant from A and B. What is the locus of the path traced out by the pcint P?
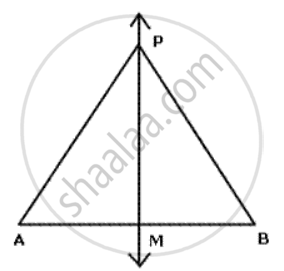
Draw and describe the lorus in the following cases:
The lorus of points inside a circle and equidistant from two fixed points on the circle .
Construct a triangle BPC given BC = 5 cm, BP = 4 cm and .
i) complete the rectangle ABCD such that:
a) P is equidistant from AB and BCV
b) P is equidistant from C and D.
ii) Measure and record the length of AB.
