Advertisements
Advertisements
प्रश्न
Draw and describe the locus in the following cases :
The locus of a point in the rhombus ABCD which is equidistant from the point A and C
उत्तर
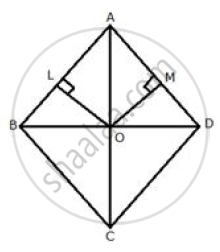
Diagonal AC and BD bisect each other at right angles at O.
Hence, O is equidistant from A and C.
APPEARS IN
संबंधित प्रश्न
Construct a triangle ABC, with AB = 5.6 cm, AC = BC = 9.2 cm. Find the points equidistant from AB and AC; and also 2 cm from BC. Measure the distance between the two points obtained.
Use graph paper for this question. Take 2 cm = 1 unit on both the axes.
- Plot the points A(1, 1), B(5, 3) and C(2, 7).
- Construct the locus of points equidistant from A and B.
- Construct the locus of points equidistant from AB and AC.
- Locate the point P such that PA = PB and P is equidistant from AB and AC.
- Measure and record the length PA in cm.
Two straight roads AB and CD cross each other at Pat an angle of 75° . X is a stone on the road AB, 800m from P towards B. BY taking an appropriate scale draw a figure to locate the position of a pole, which is equidistant from P and X, and is also equidistant from the roads.
Construct a Δ XYZ in which XY= 4 cm, YZ = 5 cm and ∠ Y = 1200. Locate a point T such that ∠ YXT is a right angle and Tis equidistant from Y and Z. Measure TZ.
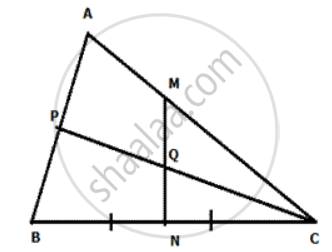
In the given figure ABC is a triangle. CP bisects angle ACB and MN is perpendicular bisector of BC. MN cuts CP at Q. Prove Q is equidistant from B and C, and also that Q is equidistant from BC and AC.
In given figure 1 ABCD is an arrowhead. AB = AD and BC = CD. Prove th at AC produced bisects BD at right angles at the point M

In Δ PQR, bisectors of ∠ PQR and ∠ PRQ meet at I. Prove that I is equidistant from the three sides of the triangle , and PI bisects ∠ QPR .
Construct a triangle ABC, such that AB= 6 cm, BC= 7.3 cm and CA= 5.2 cm. Locate a point which is equidistant from A, B and C.
State and draw the locus of a swimmer maintaining the same distance from a lighthouse.
Use ruler and compass to answer this question. Construct ∠ABC = 90°, where AB = 6 cm, BC = 8 cm.
- Construct the locus of points equidistant from B and C.
- Construct the locus of points equidistant from A and B.
- Mark the point which satisfies both the conditions (a) and (b) as 0. Construct the locus of points keeping a fixed distance OA from the fixed point 0.
- Construct the locus of points which are equidistant from BA and BC.
