Advertisements
Advertisements
प्रश्न
Draw and describe the locus in the following cases :
The locus of a point in the rhombus ABCD which is equidistant from the point A and C
उत्तर
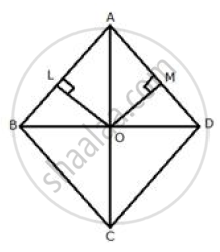
Diagonal AC and BD bisect each other at right angles at O.
Hence, O is equidistant from A and C.
APPEARS IN
संबंधित प्रश्न
Construct a triangle ABC with AB = 5.5 cm, AC = 6 cm and ∠BAC = 105°
Hence:
1) Construct the locus of points equidistant from BA and BC
2) Construct the locus of points equidistant from B and C.
3) Mark the point which satisfies the above two loci as P. Measure and write the length of PC.
Construct an isosceles triangle ABC such that AB = 6 cm, BC = AC = 4 cm. Bisect ∠C internally and mark a point P on this bisector such that CP = 5 cm. Find the points Q and R which are 5 cm from P and also 5 cm from the line AB.
AB and CD are two intersecting lines. Find a point equidistant from AB and CD, and also at a distance of 1.8 cm from another given line EF.
Construct a Δ XYZ in which XY= 4 cm, YZ = 5 cm and ∠ Y = 1200. Locate a point T such that ∠ YXT is a right angle and Tis equidistant from Y and Z. Measure TZ.
Draw and describe the lorus in the following cases:
The Iocus of the mid-points of all parallel chords of a circle.
Draw and describe the lorus in the following cases:
The lorus of a point in rhombus ABCD which is equidistant from AB and AD .
Without using set squares or protractor construct a triangle ABC in which AB = 4 cm, BC = 5 cm and ∠ABC = 120°.
(i) Locate the point P such that ∠BAp = 90° and BP = CP.
(ii) Measure the length of BP.
State and draw the locus of a point equidistant from two given parallel lines.
Without using set squares or protractor construct:
(i) Triangle ABC, in which AB = 5.5 cm, BC = 3.2 cm and CA = 4.8 cm.
(ii) Draw the locus of a point which moves so that it is always 2.5 cm from B.
(iii) Draw the locus of a point which moves so that it is equidistant from the sides BC and CA.
(iv) Mark the point of intersection of the loci with the letter P and measure PC.
Ruler and compass only may be used in this question. All construction lines and arcs must be clearly shown, and be of sufficient length and clarity to permit assessment.
(i) Construct Δ ABC, in which BC = 8 cm, AB = 5 cm, ∠ ABC = 60°.
(ii) Construct the locus of point inside the triangle which are equidistant from BA and BC.
(iii) Construct the locus of points inside the triangle which are equidistant from B and C.
(iv) Mark as P, the point which is equidistant from AB, BC and also equidistant from B and C.
(v) Measure and record the length of PB.
