Advertisements
Advertisements
प्रश्न
Describe completely the locus of point in the following cases:
Midpoint of radii of a circle.
उत्तर
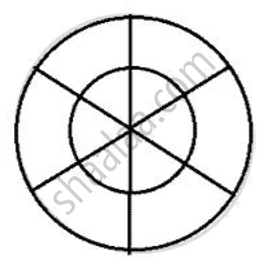
The locus of mid-point of radii of a circle is a concentric circle of radius equal to half the radius of given circle.
APPEARS IN
संबंधित प्रश्न
On a graph paper, draw the lines x = 3 and y = –5. Now, on the same graph paper, draw the locus of the point which is equidistant from the given lines.
Describe the locus of a point in space, which is always at a distance of 4 cm from a fixed point.
Construct a rhombus ABCD whose diagonals AC and BD are 8 cm and 6 cm respectively. Find by construction a point P equidistant from AB and AD and also from C and D.
In given figure, ABCD is a kite. AB = AD and BC =CD. Prove that the diagona AC is the perpendirular bisector of the diagonal BD.
In Δ PQR, bisectors of ∠ PQR and ∠ PRQ meet at I. Prove that I is equidistant from the three sides of the triangle , and PI bisects ∠ QPR .
Draw and describe the lorus in the following cases:
The lorus of points inside a circle and equidistant from two fixed points on the circle .
Describe completely the locus of points in the following cases:
Centre of a circle of varying radius and touching the two arms of ∠ ABC.
State and draw the locus of a swimmer maintaining the same distance from a lighthouse.
Using only a ruler and compass construct ∠ABC = 120°, where AB = BC = 5 cm.
(i) Mark two points D and E which satisfy the condition that they are equidistant from both ABA and BC.
(ii) In the above figure, join AD, DC, AE and EC. Describe the figures:
(a) AECB, (b) ABD, (c) ABE.
Use ruler and compasses only for this question. Draw a circle of radius 4 cm and mark two chords AB and AC of the circle of length f 6 cm and 5 cm respectively.
(i) Construct the locus of points, inside the circle, that are equidistant from A and C. Prove your construction.
(ii) Construct the locus of points, inside the circle, that are equidistant from AB and AC.
