Advertisements
Advertisements
प्रश्न
Describe completely the locus of points in the following cases:
Centre of a circle of varying radius and touching the two arms of ∠ ABC.
उत्तर
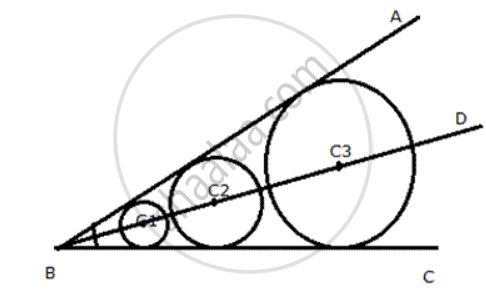
The Iocus of a cirde of varying radius and touching two arms of ∠ ABC is the bisector of that angle.
APPEARS IN
संबंधित प्रश्न
On a graph paper, draw the line x = 6. Now, on the same graph paper, draw the locus of the point which moves in such a way that its distantce from the given line is always equal to 3 units
Describe the locus of a point P, so that:
AB2 = AP2 + BP2,
where A and B are two fixed points.
O is a fixed point. Point P moves along a fixed line AB. Q is a point on OP produced such that OP = PQ. Prove that the locus of point Q is a line parallel to AB.
Construct a triangle BCP given BC = 5 cm, BP = 4 cm and ∠PBC = 45°.
- Complete the rectangle ABCD such that:
- P is equidistant from AB and BC.
- P is equidistant from C and D.
- Measure and record the length of AB.
In Δ ABC, B and Care fixed points. Find the locus of point A which moves such that the area of Δ ABC remains the same.
Draw and describe the lorus in the following cases:
The lorus of a point in rhombus ABCD which is equidistant from AB and AD .
State and draw the locus of a swimmer maintaining the same distance from a lighthouse.
State and draw the locus of a point equidistant from two given parallel lines.
Construct a Δ ABC, with AB = 6 cm, AC = BC = 9 cm; find a point 4 cm from A and equidistant from B and C.
Using ruler and compasses construct:
(i) a triangle ABC in which AB = 5.5 cm, BC = 3.4 cm and CA = 4.9 cm.
(ii) the locus of point equidistant from A and C.
(iii) a circle touching AB at A and passing through C.
