Advertisements
Advertisements
प्रश्न
Construct a Δ ABC, with AB = 6 cm, AC = BC = 9 cm; find a point 4 cm from A and equidistant from B and C.
उत्तर
Construct the ΔABC with given measurements. Draw perpendicular bisector of BC.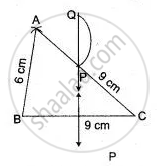
With A as centre and 4 cm as radius, draw an arc to intersect perpendicular bisector at P and Q.
Then the points P and Q are the requisite points.
APPEARS IN
संबंधित प्रश्न
Construct a triangle BCP given BC = 5 cm, BP = 4 cm and ∠PBC = 45°.
- Complete the rectangle ABCD such that:
- P is equidistant from AB and BC.
- P is equidistant from C and D.
- Measure and record the length of AB.
Draw two intersecting lines to include an angle of 30°. Use ruler and compasses to locate points which are equidistant from these Iines and also 2 cm away from their point of intersection. How many such points exist?
Construct a rhombus ABCD with sides of length 5 cm and diagonal AC of length 6 cm. Measure ∠ ABC. Find the point R on AD such that RB = RC. Measure the length of AR.
Construct a ti.PQR, in which PQ=S. 5 cm, QR=3. 2 cm and PR=4.8 cm. Draw the locus of a point which moves so that it is always 2.5 cm from Q.
In Δ ABC, B and Care fixed points. Find the locus of point A which moves such that the area of Δ ABC remains the same.
Describe completely the locus of point in the following cases:
Centre of a ball, rolling along a straight line on a level floor.
Describe completely the locus of points in the following cases:
Centre of a cirde of radius 2 cm and touching a fixed circle of radius 3 cm with centre O.
State and draw the locus of a swimmer maintaining the same distance from a lighthouse.
Using only a ruler and compass construct ∠ABC = 120°, where AB = BC = 5 cm.
(i) Mark two points D and E which satisfy the condition that they are equidistant from both ABA and BC.
(ii) In the above figure, join AD, DC, AE and EC. Describe the figures:
(a) AECB, (b) ABD, (c) ABE.
Use ruler and compass to answer this question. Construct ∠ABC = 90°, where AB = 6 cm, BC = 8 cm.
- Construct the locus of points equidistant from B and C.
- Construct the locus of points equidistant from A and B.
- Mark the point which satisfies both the conditions (a) and (b) as 0. Construct the locus of points keeping a fixed distance OA from the fixed point 0.
- Construct the locus of points which are equidistant from BA and BC.
