Advertisements
Advertisements
Question
Construct a Δ ABC, with AB = 6 cm, AC = BC = 9 cm; find a point 4 cm from A and equidistant from B and C.
Solution
Construct the ΔABC with given measurements. Draw perpendicular bisector of BC.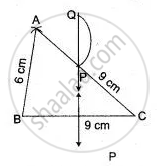
With A as centre and 4 cm as radius, draw an arc to intersect perpendicular bisector at P and Q.
Then the points P and Q are the requisite points.
APPEARS IN
RELATED QUESTIONS
Construct a triangle ABC, with AB = 5.6 cm, AC = BC = 9.2 cm. Find the points equidistant from AB and AC; and also 2 cm from BC. Measure the distance between the two points obtained.
Construct an isosceles triangle ABC such that AB = 6 cm, BC = AC = 4 cm. Bisect ∠C internally and mark a point P on this bisector such that CP = 5 cm. Find the points Q and R which are 5 cm from P and also 5 cm from the line AB.
Two straight roads AB and CD cross each other at Pat an angle of 75° . X is a stone on the road AB, 800m from P towards B. BY taking an appropriate scale draw a figure to locate the position of a pole, which is equidistant from P and X, and is also equidistant from the roads.
A and B are fixed points while Pis a moving point, moving in a way that it is always equidistant from A and B. What is the locus of the path traced out by the pcint P?
Draw and describe the lorus in the following cases:
The locus of points at a distance of 4 cm from a fixed line.
Draw and describe the lorus in the following cases:
The lorus of a point in rhombus ABCD which is equidistant from AB and AD .
Describe completely the locus of point in the following cases:
Midpoint of radii of a circle.
State and draw the locus of a swimmer maintaining the same distance from a lighthouse.
Without using set squares or protractor.
(i) Construct a ΔABC, given BC = 4 cm, angle B = 75° and CA = 6 cm.
(ii) Find the point P such that PB = PC and P is equidistant from the side BC and BA. Measure AP.
Given ∠BAC (Fig), determine the locus of a point which lies in the interior of ∠BAC and equidistant from two lines AB and AC.
