Advertisements
Advertisements
Question
Draw and describe the lorus in the following cases:
The locus of points at a distance of 4 cm from a fixed line.
Solution
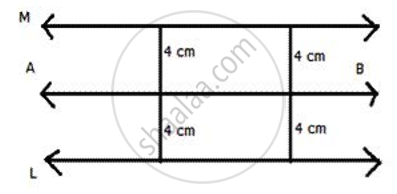
The locus of points at a distance of 4 cm from fixed line AB are lines Land M which are parallel to AB.
APPEARS IN
RELATED QUESTIONS
Use ruler and compasses only for this question:
I. Construct ABC, where AB = 3.5 cm, BC = 6 cm and ABC = 60o.
II. Construct the locus of points inside the triangle which are equidistant from BA and BC.
III. Construct the locus of points inside the triangle which are equidistant from B and C.
IV. Mark the point P which is equidistant from AB, BC and also equidistant from B and C. Measure and records the length of PB.
On a graph paper, draw the line x = 6. Now, on the same graph paper, draw the locus of the point which moves in such a way that its distantce from the given line is always equal to 3 units
Ruler and compasses may be used in this question. All construction lines and arcs must be clearly shown and be of sufficient length and clarity to permit assessment.
- Construct a ΔABC, in which BC = 6 cm, AB = 9 cm and angle ABC = 60°.
- Construct the locus of all points inside triangle ABC, which are equidistant from B and C.
- Construct the locus of the vertices of the triangles with BC as base and which are equal in area to triangle ABC.
- Mark the point Q, in your construction, which would make ΔQBC equal in area to ΔABC, and isosceles.
- Measure and record the length of CQ.
Use ruler and compasses only for this question. Draw a circle of radius 4 cm and mark two chords AB and AC of the circle of lengths 6 cm and 5 cm respectively.
(i) Construct the locus of points, inside the circle, that are equidistant from A and C. prove your construction.
(ii) Construct the locus of points, inside the circle that are equidistant from AB and AC.
Construct a rhombus ABCD whose diagonals AC and BD are 8 cm and 6 cm respectively. Find by construction a point P equidistant from AB and AD and also from C and D.
Describe completely the locus of point in the following cases:
Midpoint of radii of a circle.
Construct a Δ ABC, with AB = 6 cm, AC = BC = 9 cm; find a point 4 cm from A and equidistant from B and C.
How will you find a point equidistant from three given points A, B, C which are not in the same straight line?
Without using set squares or protractor.
(i) Construct a ΔABC, given BC = 4 cm, angle B = 75° and CA = 6 cm.
(ii) Find the point P such that PB = PC and P is equidistant from the side BC and BA. Measure AP.
Given ∠BAC (Fig), determine the locus of a point which lies in the interior of ∠BAC and equidistant from two lines AB and AC.
