Advertisements
Advertisements
Question
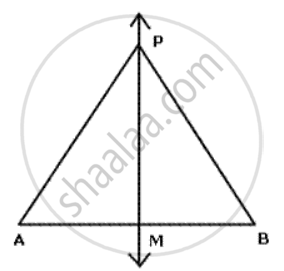
Given ∠BAC (Fig), determine the locus of a point which lies in the interior of ∠BAC and equidistant from two lines AB and AC.
Advertisements
Solution
Given: ∠BAC and an interior point P lying in the interior of ∠BAC such that PM = PN.
Construction: Join Ao and produced it to X.
Proof: In right Δs APM and APN we have
PM = PN ...[Given]
AP = AP ...[Common]
So, by RHS criterion of congruence
ΔAPM = ΔAPN
⇒ ∠PAM = ∠PAN ...[∵ Corresponding parts of congruent triangle are equal]
⇒ AP is the bisector of ∠BAC
⇒ P lies on the bisector of ∠BAC
Hence, the locus of P is the bisector of ∠BAc.
Now, we shall show that every point on the bisector of ∠BAC is equidistant from AB and AC.
So, let P be a point on the bisector AX of ∠BAC and PM ⊥ AB and PN ⊥ AC. Then, we have to prove that Pm = PN.
In Δs PAM and PAN, we have
∠PAM = ∠PAN ...[∵ AX is the bisector of ∠A]
∠PMA = ∠PNA ...[Each equal to 90°]
and AP = AP ...[Common]
So, by AAS criterion of congruence
ΔPAM = ΔPAN
⇒ PM = PN ...[∵ Corresponding parts of congruent triangles are equal]
Hence, the locus of point P is the ray AX which is the bisector of ∠BAC.
RELATED QUESTIONS
Describe the locus of a point P, so that:
AB2 = AP2 + BP2,
where A and B are two fixed points.
Draw an angle ABC = 75°. Find a point P such that P is at a distance of 2 cm from AB and 1.5 cm from BC.
Construct a triangle ABC, with AB = 5.6 cm, AC = BC = 9.2 cm. Find the points equidistant from AB and AC; and also 2 cm from BC. Measure the distance between the two points obtained.
Ruler and compasses may be used in this question. All construction lines and arcs must be clearly shown and be of sufficient length and clarity to permit assessment.
- Construct a ΔABC, in which BC = 6 cm, AB = 9 cm and angle ABC = 60°.
- Construct the locus of all points inside triangle ABC, which are equidistant from B and C.
- Construct the locus of the vertices of the triangles with BC as base and which are equal in area to triangle ABC.
- Mark the point Q, in your construction, which would make ΔQBC equal in area to ΔABC, and isosceles.
- Measure and record the length of CQ.
Draw a straight line AB of 9 cm. Draw the locus of all points which are equidistant from A and B. Prove your statement.
Using a ruler and compass only:
(i) Construct a triangle ABC with BC = 6 cm, ∠ABC = 120° and AB = 3.5 cm.
(ii) In the above figure, draw a circle with BC as diameter. Find a point 'P' on the circumference of the circle which is equidistant from Ab and BC.
Measure ∠BCP.
Without using set squares or a protractor, construct:
- Triangle ABC, in which AB = 5.5 cm, BC = 3.2 cm and CA = 4.8 cm.
- Draw the locus of a point which moves so that it is always 2.5 cm from B.
- Draw the locus of a point which moves so that it is equidistant from the sides BC and CA.
- Mark the point of intersection of the loci with the letter P and measure PC.
Use ruler and compasses only for this question. Draw a circle of radius 4 cm and mark two chords, AB and AC, of the circle of length 6 cm and 5 cm respectively.
- Construct the locus of points, inside the circle, that are equidistant from A and C. Prove your construction.
- Construct the locus of points, inside the circle, that are equidistant from AB and AC.
Ruler and compass only may be used in this question. All construction lines and arcs must be clearly shown, and be of sufficient length and clarity to permit assessment.
(i) Construct Δ ABC, in which BC = 8 cm, AB = 5 cm, ∠ ABC = 60°.
(ii) Construct the locus of point inside the triangle which are equidistant from BA and BC.
(iii) Construct the locus of points inside the triangle which are equidistant from B and C.
(iv) Mark as P, the point which is equidistant from AB, BC and also equidistant from B and C.
(v) Measure and record the length of PB.
Ruler and compasses only may be used in this question. All construction lines and arcs must be clearly shown, and be of sufficient length and clarity to permit assessment.
(i) Construct a ΔABC, in which BC = 6 cm, AB = 9 cm and ∠ABC = 60°.
(ii) Construct the locus of the vertices of the triangles with BC as base, which are equal in area to ΔABC.
(iii) Mark the point Q, in your construction, which would make ΔQBC equal in area to ΔABC, and isosceles.
(iv) Measure and record the length of CQ.
