Advertisements
Advertisements
Question
Draw an angle ABC = 75°. Find a point P such that P is at a distance of 2 cm from AB and 1.5 cm from BC.
Solution
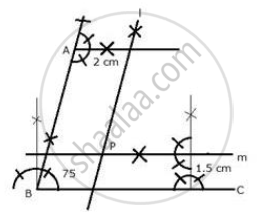
Steps of construction:
- Draw a ray BC.
- At B, draw a ray BA making an angle of 75° with BC.
- Draw a line l parallel to AB at a distance of 2 cm
- Draw another line m parallel to BC at a distance of 1.5 cm which intersects line l at P.
P is the required point.
APPEARS IN
RELATED QUESTIONS
Use graph paper for this question. Take 2 cm = 1 unit on both the axes.
- Plot the points A(1, 1), B(5, 3) and C(2, 7).
- Construct the locus of points equidistant from A and B.
- Construct the locus of points equidistant from AB and AC.
- Locate the point P such that PA = PB and P is equidistant from AB and AC.
- Measure and record the length PA in cm.
Draw two intersecting lines to include an angle of 30°. Use ruler and compasses to locate points which are equidistant from these Iines and also 2 cm away from their point of intersection. How many such points exist?
AB and CD are two intersecting lines. Find a point equidistant from AB and CD, and also at a distance of 1.8 cm from another given line EF.
In Δ PQR, s is a point on PR such that ∠ PQS = ∠ RQS . Prove thats is equidistant from PQ and QR.
In given figure 1 ABCD is an arrowhead. AB = AD and BC = CD. Prove th at AC produced bisects BD at right angles at the point M

Describe completely the locus of point in the following cases:
Centre of a ball, rolling along a straight line on a level floor.
Using only a ruler and compass construct ∠ABC = 120°, where AB = BC = 5 cm.
(i) Mark two points D and E which satisfy the condition that they are equidistant from both ABA and BC.
(ii) In the above figure, join AD, DC, AE and EC. Describe the figures:
(a) AECB, (b) ABD, (c) ABE.
Without using set squares or protractor construct:
(i) Triangle ABC, in which AB = 5.5 cm, BC = 3.2 cm and CA = 4.8 cm.
(ii) Draw the locus of a point which moves so that it is always 2.5 cm from B.
(iii) Draw the locus of a point which moves so that it is equidistant from the sides BC and CA.
(iv) Mark the point of intersection of the loci with the letter P and measure PC.
Ruler and compasses only may be used in this question. All construction lines and arcs must be clearly shown, and be of sufficient length and clarity to permit assessment.
(i) Construct a ΔABC, in which BC = 6 cm, AB = 9 cm and ∠ABC = 60°.
(ii) Construct the locus of the vertices of the triangles with BC as base, which are equal in area to ΔABC.
(iii) Mark the point Q, in your construction, which would make ΔQBC equal in area to ΔABC, and isosceles.
(iv) Measure and record the length of CQ.
Use ruler and compass to answer this question. Construct ∠ABC = 90°, where AB = 6 cm, BC = 8 cm.
- Construct the locus of points equidistant from B and C.
- Construct the locus of points equidistant from A and B.
- Mark the point which satisfies both the conditions (a) and (b) as 0. Construct the locus of points keeping a fixed distance OA from the fixed point 0.
- Construct the locus of points which are equidistant from BA and BC.
