Advertisements
Advertisements
प्रश्न
Draw an angle ABC = 75°. Find a point P such that P is at a distance of 2 cm from AB and 1.5 cm from BC.
उत्तर
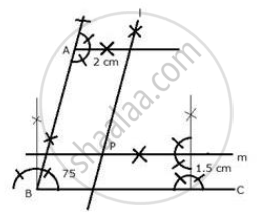
Steps of construction:
- Draw a ray BC.
- At B, draw a ray BA making an angle of 75° with BC.
- Draw a line l parallel to AB at a distance of 2 cm
- Draw another line m parallel to BC at a distance of 1.5 cm which intersects line l at P.
P is the required point.
APPEARS IN
संबंधित प्रश्न
Describe the locus of vertices of all isosceles triangles having a common base.
Angle ABC = 60° and BA = BC = 8 cm. The mid-points of BA and BC are M and N respectively. Draw and describe the locus of a point which is:
- equidistant from BA and BC.
- 4 cm from M.
- 4 cm from N.
Mark the point P, which is 4 cm from both M and N, and equidistant from BA and BC. Join MP and NP, and describe the figure BMPN.
State the locus of a point in a rhombus ABCD, which is equidistant
- from AB and AD;
- from the vertices A and C.
Plot the points A(2, 9), B(–1, 3) and C(6, 3) on graph paper. On the same graph paper draw the locus of point A so that the area of ΔABC remains the same as A moves.
Draw two intersecting lines to include an angle of 30°. Use ruler and compasses to locate points which are equidistant from these Iines and also 2 cm away from their point of intersection. How many such points exist?
A and B are fixed points while Pis a moving point, moving in a way that it is always equidistant from A and B. What is the locus of the path traced out by the pcint P?
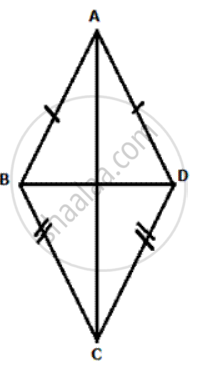
In given figure, ABCD is a kite. AB = AD and BC =CD. Prove that the diagona AC is the perpendirular bisector of the diagonal BD.
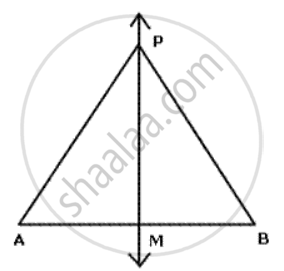
Draw and describe the lorus in the following cases:
The locus of points at a distance of 4 cm from a fixed line.
Draw and describe the locus in the following cases :
The locus of a point in the rhombus ABCD which is equidistant from the point A and C
Given ∠BAC (Fig), determine the locus of a point which lies in the interior of ∠BAC and equidistant from two lines AB and AC.
