Advertisements
Advertisements
Question
How will you find a point equidistant from three given points A, B, C which are not in the same straight line?
Solution
(i) The locus of points equidistant from three given points A, B & C is the straight line PQ, which bisects AB at right angles.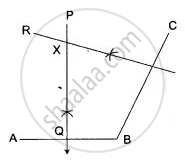
(ii) Similarly, the locus of points equidistant from B and C is the straight line RS which bisects BC at right angles.
Hence, the point common to PQ and RS must satisfy both conditions; that is to say, X the point of intersection of PQ and RS will be equidistant from A, B and C.
APPEARS IN
RELATED QUESTIONS
O is a fixed point. Point P moves along a fixed line AB. Q is a point on OP produced such that OP = PQ. Prove that the locus of point Q is a line parallel to AB.
Draw a straight line AB of 9 cm. Draw the locus of all points which are equidistant from A and B. Prove your statement.
Construct a rhombus ABCD with sides of length 5 cm and diagonal AC of length 6 cm. Measure ∠ ABC. Find the point R on AD such that RB = RC. Measure the length of AR.
In Δ PQR, s is a point on PR such that ∠ PQS = ∠ RQS . Prove thats is equidistant from PQ and QR.
Draw and describe the lorus in the following cases:
The lorus of a point in rhombus ABCD which is equidistant from AB and AD .
Describe completely the locus of points in the following cases:
Point in a plane equidistant from a given line.
Without using set squares or protractor construct a triangle ABC in which AB = 4 cm, BC = 5 cm and ∠ABC = 120°.
(i) Locate the point P such that ∠BAp = 90° and BP = CP.
(ii) Measure the length of BP.
Using only a ruler and compass construct ∠ABC = 120°, where AB = BC = 5 cm.
(i) Mark two points D and E which satisfy the condition that they are equidistant from both ABA and BC.
(ii) In the above figure, join AD, DC, AE and EC. Describe the figures:
(a) AECB, (b) ABD, (c) ABE.
Use ruler and compasses only for the following questions:
Construct triangle BCP, when CB = 5 cm, BP = 4 cm, ∠PBC = 45°.
Complete the rectangle ABCD such that :
(i) P is equidistant from AB and BC and
(ii) P is equidistant from C and D. Measure and write down the length of AB.
Given ∠BAC (Fig), determine the locus of a point which lies in the interior of ∠BAC and equidistant from two lines AB and AC.
