Advertisements
Advertisements
Question
Describe completely the locus of points in the following cases:
Point in a plane equidistant from a given line.
Solution
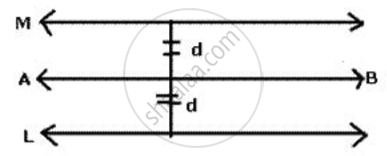
The locus of all points in a plane equidistant from a fixed line is represented by two parallel lines either side of it at a distanced away.
APPEARS IN
RELATED QUESTIONS
O is a fixed point. Point P moves along a fixed line AB. Q is a point on OP produced such that OP = PQ. Prove that the locus of point Q is a line parallel to AB.
Construct a triangle ABC, with AB = 5.6 cm, AC = BC = 9.2 cm. Find the points equidistant from AB and AC; and also 2 cm from BC. Measure the distance between the two points obtained.
Plot the points A(2, 9), B(–1, 3) and C(6, 3) on graph paper. On the same graph paper draw the locus of point A so that the area of ΔABC remains the same as A moves.
Construct a triangle BCP given BC = 5 cm, BP = 4 cm and ∠PBC = 45°.
- Complete the rectangle ABCD such that:
- P is equidistant from AB and BC.
- P is equidistant from C and D.
- Measure and record the length of AB.
Construct a rhombus ABCD with sides of length 5 cm and diagonal AC of length 6 cm. Measure ∠ ABC. Find the point R on AD such that RB = RC. Measure the length of AR.
In given figure 1 ABCD is an arrowhead. AB = AD and BC = CD. Prove th at AC produced bisects BD at right angles at the point M

In Δ ABC, B and Care fixed points. Find the locus of point A which moves such that the area of Δ ABC remains the same.
Draw and describe the lorus in the following cases:
The Iocus of the mid-points of all parallel chords of a circle.
Using only ruler and compasses, construct a triangle ABC 1 with AB = 5 cm, BC = 3.5 cm and AC= 4 cm. Mark a point P, which is equidistant from AB, BC and also from Band C. Measure the length of PB.
Using ruler and compasses construct:
(i) a triangle ABC in which AB = 5.5 cm, BC = 3.4 cm and CA = 4.9 cm.
(ii) the locus of point equidistant from A and C.
(iii) a circle touching AB at A and passing through C.
