Advertisements
Advertisements
प्रश्न
On a graph paper, draw the line x = 6. Now, on the same graph paper, draw the locus of the point which moves in such a way that its distantce from the given line is always equal to 3 units
उत्तर
 On the graph, draw axis XOX’ and YOY’
On the graph, draw axis XOX’ and YOY’
Draw a line l, x = 6 which is parallel to y-axis
Take points P and Q which are at a distance of 3 units from the line l.
Draw lines m and n from P and Q parallel to l
With locus = 3, two lines can be drawn x = 3 and x = 9.
APPEARS IN
संबंधित प्रश्न
Use ruler and compasses only for this question:
I. Construct ABC, where AB = 3.5 cm, BC = 6 cm and ABC = 60o.
II. Construct the locus of points inside the triangle which are equidistant from BA and BC.
III. Construct the locus of points inside the triangle which are equidistant from B and C.
IV. Mark the point P which is equidistant from AB, BC and also equidistant from B and C. Measure and records the length of PB.
Describe the locus of vertices of all isosceles triangles having a common base.
Describe the locus of a point P, so that:
AB2 = AP2 + BP2,
where A and B are two fixed points.
In given figure, ABCD is a kite. AB = AD and BC =CD. Prove that the diagona AC is the perpendirular bisector of the diagonal BD.
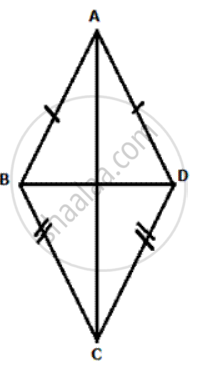
In given figure 1 ABCD is an arrowhead. AB = AD and BC = CD. Prove th at AC produced bisects BD at right angles at the point M

Describe completely the locus of points in the following cases:
Point in a plane equidistant from a given line.
Construct a Δ ABC, with AB = 6 cm, AC = BC = 9 cm; find a point 4 cm from A and equidistant from B and C.
Using a ruler and compass only:
(i) Construct a triangle ABC with BC = 6 cm, ∠ABC = 120° and AB = 3.5 cm.
(ii) In the above figure, draw a circle with BC as diameter. Find a point 'P' on the circumference of the circle which is equidistant from Ab and BC.
Measure ∠BCP.
Use ruler and compasses only for the following questions:
Construct triangle BCP, when CB = 5 cm, BP = 4 cm, ∠PBC = 45°.
Complete the rectangle ABCD such that :
(i) P is equidistant from AB and BC and
(ii) P is equidistant from C and D. Measure and write down the length of AB.
Use ruler and compass to answer this question. Construct ∠ABC = 90°, where AB = 6 cm, BC = 8 cm.
- Construct the locus of points equidistant from B and C.
- Construct the locus of points equidistant from A and B.
- Mark the point which satisfies both the conditions (a) and (b) as 0. Construct the locus of points keeping a fixed distance OA from the fixed point 0.
- Construct the locus of points which are equidistant from BA and BC.
