Advertisements
Advertisements
प्रश्न
Use ruler and compasses only for this question:
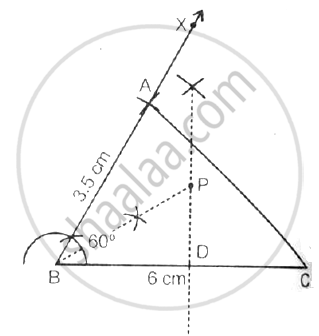
I. Construct ABC, where AB = 3.5 cm, BC = 6 cm and ABC = 60o.
II. Construct the locus of points inside the triangle which are equidistant from BA and BC.
III. Construct the locus of points inside the triangle which are equidistant from B and C.
IV. Mark the point P which is equidistant from AB, BC and also equidistant from B and C. Measure and records the length of PB.
उत्तर
Steps of constructions:
1) Draw a line BC = 6 cm and CBX = 60°. Cut off AB = 3.5 cm. Join AC, ΔABC is the required triangle.
2) Draw perpendicular bisector of BC and bisector of ∠B.
3) The bisector of ∠B meets bisector of BC at P, therefore BP is the required length,
Where BP = 3.5 cm
4) P is the point which is equidistant from BA and BC, also equidistant from B and C.
APPEARS IN
संबंधित प्रश्न
Use ruler and compasses only for this question. Draw a circle of radius 4 cm and mark two chords AB and AC of the circle of lengths 6 cm and 5 cm respectively.
(i) Construct the locus of points, inside the circle, that are equidistant from A and C. prove your construction.
(ii) Construct the locus of points, inside the circle that are equidistant from AB and AC.
Draw two intersecting lines to include an angle of 30°. Use ruler and compasses to locate points which are equidistant from these Iines and also 2 cm away from their point of intersection. How many such points exist?
AB and CD are two intersecting lines. Find a point equidistant from AB and CD, and also at a distance of 1.8 cm from another given line EF.
In given figure, ABCD is a kite. AB = AD and BC =CD. Prove that the diagona AC is the perpendirular bisector of the diagonal BD.
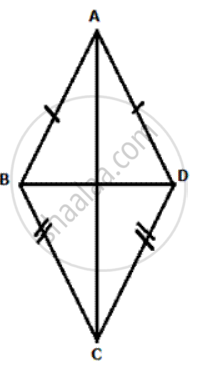
In given figure 1 ABCD is an arrowhead. AB = AD and BC = CD. Prove th at AC produced bisects BD at right angles at the point M

In Δ ABC, B and Care fixed points. Find the locus of point A which moves such that the area of Δ ABC remains the same.
Draw and describe the lorus in the following cases:
The Iocus of the mid-points of all parallel chords of a circle.
Describe completely the locus of points in the following cases:
Centre of a circle of varying radius and touching the two arms of ∠ ABC.
Describe completely the locus of points in the following cases:
Centre of a cirde of radius 2 cm and touching a fixed circle of radius 3 cm with centre O.
Given ∠BAC (Fig), determine the locus of a point which lies in the interior of ∠BAC and equidistant from two lines AB and AC.
