Advertisements
Advertisements
प्रश्न
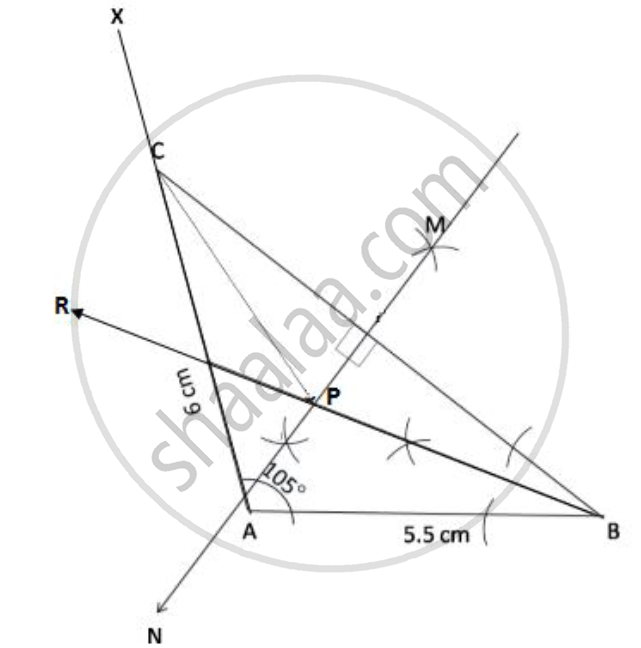
Construct a triangle ABC with AB = 5.5 cm, AC = 6 cm and ∠BAC = 105°
Hence:
1) Construct the locus of points equidistant from BA and BC
2) Construct the locus of points equidistant from B and C.
3) Mark the point which satisfies the above two loci as P. Measure and write the length of PC.
उत्तर
1) Draw a line segment AB of length 5.5 cm.
2) Make an angle m∠BAX = 105° using a protractor
3) Draw an arc AC with radius AC = 6 cm on AX with centre at A.
4) Join BC.
Thus ΔABC is the required triangle.
a) Draw BR, the bisector of ∠ABC, which is the locus of points equidistant from BA and BC.
b) Draw MN, the perpendicular bisector of BC, which is the locus of points equidistant from B and C
c) The angle bisector of ∠ABC and the perpendicular bisector of BC meet at point P. Thus, P satisfies the above two loci.
Length of PC = 4.8 cm
APPEARS IN
संबंधित प्रश्न
Draw an angle ABC = 75°. Find a point P such that P is at a distance of 2 cm from AB and 1.5 cm from BC.
State the locus of a point in a rhombus ABCD, which is equidistant
- from AB and AD;
- from the vertices A and C.
Use graph paper for this question. Take 2 cm = 1 unit on both the axes.
- Plot the points A(1, 1), B(5, 3) and C(2, 7).
- Construct the locus of points equidistant from A and B.
- Construct the locus of points equidistant from AB and AC.
- Locate the point P such that PA = PB and P is equidistant from AB and AC.
- Measure and record the length PA in cm.
Construct an isosceles triangle ABC such that AB = 6 cm, BC = AC = 4 cm. Bisect ∠C internally and mark a point P on this bisector such that CP = 5 cm. Find the points Q and R which are 5 cm from P and also 5 cm from the line AB.
Draw two intersecting lines to include an angle of 30°. Use ruler and compasses to locate points which are equidistant from these Iines and also 2 cm away from their point of intersection. How many such points exist?
Construct a rhombus ABCD with sides of length 5 cm and diagonal AC of length 6 cm. Measure ∠ ABC. Find the point R on AD such that RB = RC. Measure the length of AR.
In Δ ABC, B and Care fixed points. Find the locus of point A which moves such that the area of Δ ABC remains the same.
Describe completely the locus of points in the following cases:
Point in a plane equidistant from a given line.
State and draw the locus of a point equidistant from two given parallel lines.
Using a ruler and compass only:
(i) Construct a triangle ABC with BC = 6 cm, ∠ABC = 120° and AB = 3.5 cm.
(ii) In the above figure, draw a circle with BC as diameter. Find a point 'P' on the circumference of the circle which is equidistant from Ab and BC.
Measure ∠BCP.
