Advertisements
Advertisements
प्रश्न
State the locus of a point in a rhombus ABCD, which is equidistant
- from AB and AD;
- from the vertices A and C.
उत्तर
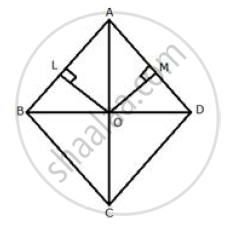
Steps of construction:
i. In rhombus ABCD, draw angle bisector of ∠A which meets in C.
ii. Join BD, which intersects AC at O.
O is the required locus.
iii. From O, draw OL ⊥ AB and OM ⊥ AD
In ΔAOL and ΔAOM
∠OLA = ∠OMA = 90°
∠OAL = ∠OAM ...(AC is bisector of angle A)
AO = OA ...(Common)
By Angle-Angle – side criterion of congruence,
ΔAOL ≅ ΔAOM ...(AAS Postulate)
The corresponding parts of the congruent triangles are congruent
`=>` OL = OM ...(C.P.C.T.)
Therefore, O is equidistant from AB and AD.
Diagonal AC and BD bisect each other at right angles at O.
Therefore, AO = OC
Hence, O is equidistant from A and C.
APPEARS IN
संबंधित प्रश्न
Construct a triangle ABC with AB = 5.5 cm, AC = 6 cm and ∠BAC = 105°
Hence:
1) Construct the locus of points equidistant from BA and BC
2) Construct the locus of points equidistant from B and C.
3) Mark the point which satisfies the above two loci as P. Measure and write the length of PC.
Without using set squares or protractor, construct a quadrilateral ABCD in which ∠ BAD = 45° , AD = AB = 6 cm, BC= 3.6 cm and CD=5 cm. Locate the point P on BD which is equidistant from BC and CD.
Construct a Δ XYZ in which XY= 4 cm, YZ = 5 cm and ∠ Y = 1200. Locate a point T such that ∠ YXT is a right angle and Tis equidistant from Y and Z. Measure TZ.
In Δ PQR, s is a point on PR such that ∠ PQS = ∠ RQS . Prove thats is equidistant from PQ and QR.
Describe completely the locus of points in the following cases:
Point in a plane equidistant from a given line.
Describe completely the locus of points in the following cases:
Centre of a circle of varying radius and touching the two arms of ∠ ABC.
Draw and describe the locus in the following cases :
The locus of a point in the rhombus ABCD which is equidistant from the point A and C
Construct a Δ ABC, with AB = 6 cm, AC = BC = 9 cm; find a point 4 cm from A and equidistant from B and C.
Using ruler and compasses construct:
(i) a triangle ABC in which AB = 5.5 cm, BC = 3.4 cm and CA = 4.9 cm.
(ii) the locus of point equidistant from A and C.
(iii) a circle touching AB at A and passing through C.
Use ruler and compasses only for this question. Draw a circle of radius 4 cm and mark two chords AB and AC of the circle of length f 6 cm and 5 cm respectively.
(i) Construct the locus of points, inside the circle, that are equidistant from A and C. Prove your construction.
(ii) Construct the locus of points, inside the circle, that are equidistant from AB and AC.
