Advertisements
Advertisements
Question
Construct a triangle BPC given BC = 5 cm, BP = 4 cm and .
i) complete the rectangle ABCD such that:
a) P is equidistant from AB and BCV
b) P is equidistant from C and D.
ii) Measure and record the length of AB.
Solution
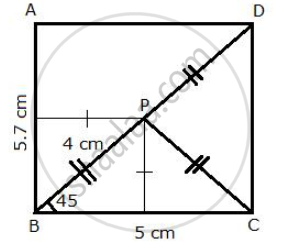
- i) Steps of Construction:
1) Draw a line segment BC = 5 cm
2) B as centre and radius 4 cm draw an arc at an angle of 45 degrees from BC.
3) Join PC.
4) B and C as centers, draw two perpendiculars to BC.
5) P as centre and radius PC, cut an arc on the perpendicular on C at D.
6) D as centre, draw a line parallel to BC which intersects the perpendicular on B at A.
ABCD is the required rectangle such that P is equidistant from AB and BC (since BD is angle bisector of angle B) as well as C and D.
- ii) On measuring AB = 5.7 cm
APPEARS IN
RELATED QUESTIONS
Use ruler and compasses only for this question:
I. Construct ABC, where AB = 3.5 cm, BC = 6 cm and ABC = 60o.
II. Construct the locus of points inside the triangle which are equidistant from BA and BC.
III. Construct the locus of points inside the triangle which are equidistant from B and C.
IV. Mark the point P which is equidistant from AB, BC and also equidistant from B and C. Measure and records the length of PB.
On a graph paper, draw the line x = 6. Now, on the same graph paper, draw the locus of the point which moves in such a way that its distantce from the given line is always equal to 3 units
Construct a triangle ABC, with AB = 6 cm, AC = BC = 9 cm. Find a point 4 cm from A and equidistant from B and C.
Use ruler and compasses only for this question. Draw a circle of radius 4 cm and mark two chords AB and AC of the circle of lengths 6 cm and 5 cm respectively.
(i) Construct the locus of points, inside the circle, that are equidistant from A and C. prove your construction.
(ii) Construct the locus of points, inside the circle that are equidistant from AB and AC.
Draw and describe the locus in the following cases :
The locus of a point in the rhombus ABCD which is equidistant from the point A and C
Construct a Δ ABC, with AB = 6 cm, AC = BC = 9 cm; find a point 4 cm from A and equidistant from B and C.
Use ruler and compasses only for this question. Draw a circle of radius 4 cm and mark two chords AB and AC of the circle of length f 6 cm and 5 cm respectively.
(i) Construct the locus of points, inside the circle, that are equidistant from A and C. Prove your construction.
(ii) Construct the locus of points, inside the circle, that are equidistant from AB and AC.
How will you find a point equidistant from three given points A, B, C which are not in the same straight line?
Without using set squares or protractor.
(i) Construct a ΔABC, given BC = 4 cm, angle B = 75° and CA = 6 cm.
(ii) Find the point P such that PB = PC and P is equidistant from the side BC and BA. Measure AP.
Use ruler and compasses only for the following questions:
Construct triangle BCP, when CB = 5 cm, BP = 4 cm, ∠PBC = 45°.
Complete the rectangle ABCD such that :
(i) P is equidistant from AB and BC and
(ii) P is equidistant from C and D. Measure and write down the length of AB.
