Advertisements
Advertisements
Question
Construct a Δ XYZ in which XY= 4 cm, YZ = 5 cm and ∠ Y = 1200. Locate a point T such that ∠ YXT is a right angle and Tis equidistant from Y and Z. Measure TZ.
Solution
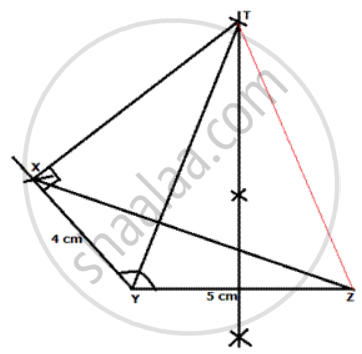
Steps of Construction:
(i) Draw YZ = 5 cm
(ii) Draw an arc with angle Y= 120 ° and radius 4 cm.
(iii) Join XZ.
(iv) Draw perpendicular bisector of YZ.
(v) With X as centre and angle X as 90° , join X to the perpendicular bisectcr at T. T is the required point.
(vi) Measure TY. TY = 6.8 cm = TZ as T lies on perpendicular bisector of YZ.
APPEARS IN
RELATED QUESTIONS
Construct a triangle ABC, with AB = 5.6 cm, AC = BC = 9.2 cm. Find the points equidistant from AB and AC; and also 2 cm from BC. Measure the distance between the two points obtained.
State the locus of a point in a rhombus ABCD, which is equidistant
- from AB and AD;
- from the vertices A and C.
Use graph paper for this question. Take 2 cm = 1 unit on both the axes.
- Plot the points A(1, 1), B(5, 3) and C(2, 7).
- Construct the locus of points equidistant from A and B.
- Construct the locus of points equidistant from AB and AC.
- Locate the point P such that PA = PB and P is equidistant from AB and AC.
- Measure and record the length PA in cm.
AB and CD are two intersecting lines. Find a point equidistant from AB and CD, and also at a distance of 1.8 cm from another given line EF.
Construct a ti.PQR, in which PQ=S. 5 cm, QR=3. 2 cm and PR=4.8 cm. Draw the locus of a point which moves so that it is always 2.5 cm from Q.
Draw and describe the lorus in the following cases:
The locus of points at a distance of 4 cm from a fixed line.
Describe completely the locus of point in the following cases:
Midpoint of radii of a circle.
Describe completely the locus of point in the following cases:
Centre of a ball, rolling along a straight line on a level floor.
State and draw the locus of a swimmer maintaining the same distance from a lighthouse.
Using ruler and compasses construct:
(i) a triangle ABC in which AB = 5.5 cm, BC = 3.4 cm and CA = 4.9 cm.
(ii) the locus of point equidistant from A and C.
(iii) a circle touching AB at A and passing through C.
