Advertisements
Advertisements
प्रश्न
Using only ruler and compasses, construct a triangle ABC 1 with AB = 5 cm, BC = 3.5 cm and AC= 4 cm. Mark a point P, which is equidistant from AB, BC and also from Band C. Measure the length of PB.
उत्तर
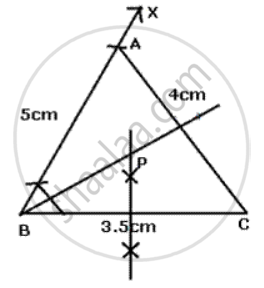
Steps of construction:
(i) Draw a line segment BC = 3. 5 cm.
(ii) With Bas centre and radius 5 cm draw an arc.
(iii) With C as centre and radius 4 cm draw another arc which intersects the first arc at A.
(iv) Join AB and AC.
(v) Dr aw perpendi cu I ar bi sector of BC.
(vi) Dr aw the angle bi sector of angle ABC which intersects the perpendicular bisector of BC at P.
Pis the required point which is equidistant from AB, BC, Band C.
The length of PB = 2.5 cm
APPEARS IN
संबंधित प्रश्न
Angle ABC = 60° and BA = BC = 8 cm. The mid-points of BA and BC are M and N respectively. Draw and describe the locus of a point which is:
- equidistant from BA and BC.
- 4 cm from M.
- 4 cm from N.
Mark the point P, which is 4 cm from both M and N, and equidistant from BA and BC. Join MP and NP, and describe the figure BMPN.
Construct a triangle ABC, with AB = 5.6 cm, AC = BC = 9.2 cm. Find the points equidistant from AB and AC; and also 2 cm from BC. Measure the distance between the two points obtained.
Two straight roads AB and CD cross each other at Pat an angle of 75° . X is a stone on the road AB, 800m from P towards B. BY taking an appropriate scale draw a figure to locate the position of a pole, which is equidistant from P and X, and is also equidistant from the roads.
Draw two intersecting lines to include an angle of 30°. Use ruler and compasses to locate points which are equidistant from these Iines and also 2 cm away from their point of intersection. How many such points exist?
Construct a rhombus ABCD with sides of length 5 cm and diagonal AC of length 6 cm. Measure ∠ ABC. Find the point R on AD such that RB = RC. Measure the length of AR.
Construct a Δ XYZ in which XY= 4 cm, YZ = 5 cm and ∠ Y = 1200. Locate a point T such that ∠ YXT is a right angle and Tis equidistant from Y and Z. Measure TZ.
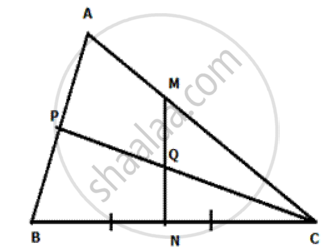
In the given figure ABC is a triangle. CP bisects angle ACB and MN is perpendicular bisector of BC. MN cuts CP at Q. Prove Q is equidistant from B and C, and also that Q is equidistant from BC and AC.
Describe completely the locus of point in the following cases:
Centre of a ball, rolling along a straight line on a level floor.
Construct a Δ ABC, with AB = 6 cm, AC = BC = 9 cm; find a point 4 cm from A and equidistant from B and C.
Use ruler and compass to answer this question. Construct ∠ABC = 90°, where AB = 6 cm, BC = 8 cm.
- Construct the locus of points equidistant from B and C.
- Construct the locus of points equidistant from A and B.
- Mark the point which satisfies both the conditions (a) and (b) as 0. Construct the locus of points keeping a fixed distance OA from the fixed point 0.
- Construct the locus of points which are equidistant from BA and BC.
